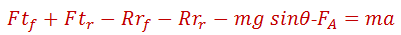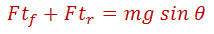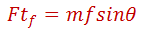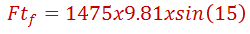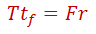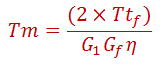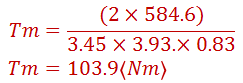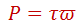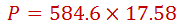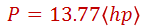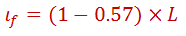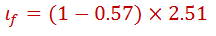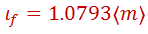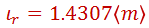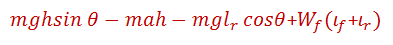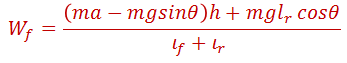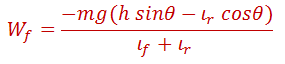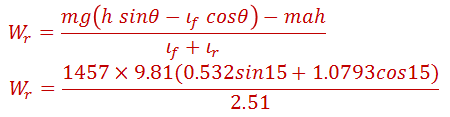4.2 Ejemplos y aplicaciones
Ejemplo 1
Determine la fuerza tractiva necesaria para que un automóvil de Jetta Clásico manual de 5 velocidades de 1.98L pueda subir una pendiente de 30 grados con 2 pasajeros a bordo. El automóvil pesa 1307 Kg en vacío y tiene una distancia entre ejes de 2.51 metros. Considerar un peso promedio de 75 Kg por pasajero. Asuma de momento que las llantas tractivas delanteras tendrán suficiente adherencia y no derraparán.
| Peso vacío (kg) |
1307 (kg) |
| Distancia entre ejes (m) |
2.51 (m) |
| Distribución de peso |
57/43 del/tras |
| Altura (m) |
1.438 (m) |
| Llantas |
205/55R16 |
| Pot Máxima @ 5200 rpm |
114 hp |
| Torque @ 1500 rpm |
250 Nm |
| Primera velocidad |
3.45 : 1 |
| Segunda velocidad |
1.95 : 1 |
| Tercera velocidad |
1.28 : 1 |
| Cuarta velocidad |
0.88 : 1 |
| Quinta velocidad |
0.67 : 1 |
| Diferencial |
3.93 : 1 |
Figura 2. Jetta Clásico 2015.
Considerando los datos del automóvil el peso total será de 1307 kg + 150 kg de los 2 pasajeros para un total de 1457 Kg. Para subir pendiente de 33% (15 grados) se necesitará un total de 3700 newton los cuales deberán ser proporcionados solamente por las llantas tractivas, que en este caso son las delanteras.
Esta fuerza indica que se necesitarán 3700 N para poder impulsar el automóvil. Dicha responsabilidad está en ambas ruedas tractivas delanteras, lo que implica 1850 N por rueda. Por otro lado, el tipo de llanta sugerido por el fabricante es 205/55R16, la cual tiene un diámetro de 632 mm; esto implica que cada rueda deberá desarrollar un par o torque de 584.6 Nm como se muestra a continuación.
El torque obtenido es solamente un torque requerido, es decir, se necesitan 584.6 Nm por rueda tractiva para que el vehículo pueda subir la pendiente de 15 grados a baja velocidad; aún y con esto, debemos indagar un poco más y obtener las limitaciones del motor a fin de averiguar si de acuerdo a sus especificaciones, éste es capaz de proporcionar el par requerido.
En el manual del propietario se indica que para un Jetta Manual de 5 velocidades, sus razones de cambio son 3.45, 1.95, 1.28, 0.88, 0.67 desde la primera hasta la quinta velocidad respectivamente; finalmente el diferencial tiene una reducción de 3.93. Entonces, tomando como ejemplo la primera velocidad, el torque requerido por rueda es de 584.6 Nm equivalente a un total de 1169 Nm totales que, vistos desde el motor, equivaldrían a 103.9 Nm como se demuestra a continuación.
Donde:
Tm : Par visto desde el motor
Ttr : Par total requerido en ruedas tractivas
G1 : Relación tren engranes (en este caso 3.45:1)
Gr : Relación del diferencial (en este caso 3.93:1)
𝜂 : eficiencia (en este caso consideraremos 83%)
Se observa que el par requerido en el motor es menor que el par máximo, esto indica que el motor especificado es suficiente para cumplir con la misión requerida, puesto que puede dar hasta 250 Nm a 1500 rpm equivalentes a una velocidad del vehículo de hasta 13.2 km/h. Por el efecto de la reducción de engranes (3.45 y 3.93), la velocidad de 1500 rpm en el motor equivale a 110 rpm (11.57 rad/s) en las ruedas considerando un radio de 316 mm en las llantas, esto equivale a una velocidad de centro de rueda de 3.66 m/s o 13.2 km/hr.
¿Qué sucede si una vez que comienza a subir, el conductor decide utilizar la segunda velocidad?
Se puede utilizar la misma expresión anterior a la reducción de la velocidad en segunda que es 1.95 (G2), y se llegará a saber que el par necesario en el motor sería de 183.61 Nm indicando que aún es posible continuar subiendo la pendiente pero a una velocidad mayor correspondiente de 23 km/h. Se deja como tarea individual al participante indagar lo que sucedería en tercera velocidad (asuma la misma eficiencia de 83%).
Ejemplo 2
Estimar la potencia necesaria si se desea que el automóvil del ejemplo anterior suba la pendiente a una velocidad de 20 km/h en segunda. En el ejemplo anterior se estimó que la fuerza tractiva requerida es de 3700 N equivalente a un torque total en las ruedas de 584.6 Nm, aunque la potencia total requerida dependerá de la velocidad a la que suba de acuerdo a la expresión:
Así entonces, considerando una velocidad de 20 km/h (5.55 m/s) y dividido por el radio de 316 mm de las ruedas, equivale a una velocidad angular de 17.58 rad/sec.
Considerando el factor de eficiencia de 83% la potencia requerida de 13.77 hp en las ruedas equivale a 16.6 hp en el motor, lo cual es aún una potencia muy baja para la capacidad especificada del motor de 114 hp. Es decir, la limitación para subir una pendiente está en el torque más que en la potencia. Hasta aquí se ha discutido como obtener el par y fuerza tractiva así como la potencia necesaria para que un vehículo pueda subir una cresta. Recordemos que existen dos limitaciones, la potencia del motor y la adherencia de las llantas. Para saber si las llantas podrán aportar la adherencia suficiente durante el trayecto de un vehículo cuesta arriba, hay que tomar en cuenta varios factores: los parámetros de la llanta principalmente el límite máximo de fricción y la fuerza normal. Comenzaremos por determinar la fuerza normal.
Ejemplo 3
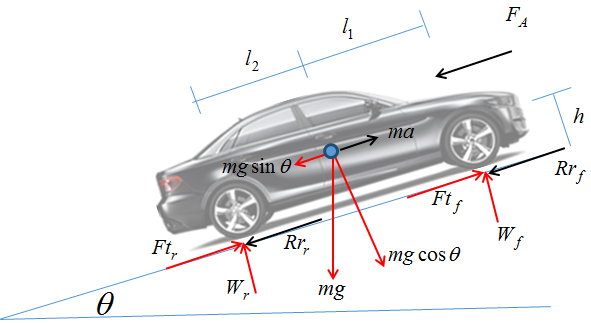
Determine la fuerza normal en las llantas tractivas del automóvil considerando los ejemplos anteriores. Nos interesa encontrar la fuerza normal de las ruedas motrices que en nuestro caso son las delanteras, entonces volviendo al diagrama de la figura 1, la variable de interés es Wf. Antes necesitamos ubicar correctamente el centro de gravedad. De acuerdo a la ficha técnica de la tabla 1, se nos indica que el automóvil tiene su peso repartido hacia adelante en un 57% (más de la mitad), entonces es necesario encontrar la ubicación del centro de gravedad con respecto a los ejes delantero (l1) y trasero (l2). El vehículo tiene una distancia entre ejes de 2.51 m que denominaremos por la variable L, entonces utilizando momentos estáticos simples se tiene lo siguiente:
Asimismo:
La altura del centro de gravedad puede ser encontrada tanto de forma experimental como de bases de datos, en este apartado utilizaremos la base de datos SAE 1999-01-1336, la cual se reproduce aquí con permiso de la Sociedad de Ingenieros Automotrices.
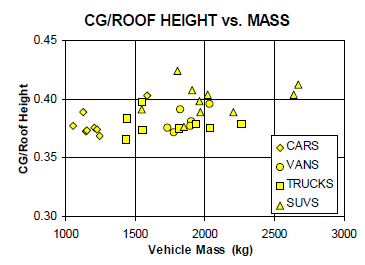
Figura 3. Altura CG/Altura vehículo, SAE 1999-01-1336.
De la figura se puede estimar que la altura del centro de gravedad para autos se encuentra aproximadamente a 37% de la altura total del vehículo, así entonces si la altura especificada del vehículo es de 1.438 m se puede estimar que la altura de su centro de gravedad estará aproximadamente a 0.532 m con respecto al piso.
A continuación se reproduce el diagrama de cuerpo libre de la figura 1 con los datos del centro de gravedad.
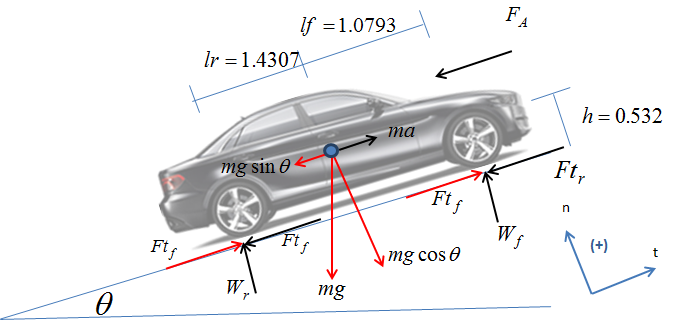
Figura 4. Diagrama de cuerpo libre con datos de centro de gravedad.
Para obtener la fuerza normal Wf en los neumáticos delanteros, se hace una suma de momentos alrededor del punto de contacto de la rueda trasera. Entonces se tiene:
La ecuación anterior indica una transferencia de carga hacia atrás debido al efecto de la aceleración, pero para nuestro caso, si asumimos que el vehículo subirá a velocidad constante, entonces se elimina el efecto de la aceleración, quedando aislado sólo el efecto de la pendiente, entonces:
Considerando los datos obtenidos:

De forma similar para las ruedas traseras, se obtiene la siguiente expresión:
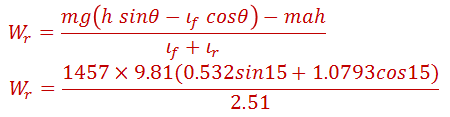
Y se obtiene como resultado:
Retomando la pregunta inicial, ¿es posible que el auto suba la pendiente de 15 grados sin derrapar?
Los cálculos obtenidos indican que la fuerza normal en el eje tractivo delantero cuando el auto está remontando una pendiente de 15 grados es de 7085N, lo cual equivale a decir que cada llanta tractiva soporta en ese instante una carga de presión de 3542 N. La figura 5 muestra cinco curvas de llantas a diferentes cargas normales; si observamos la más cercana a nuestro dato de 3542 sería la de 3995 N (curva roja mostrada en la figura); por otro lado, el rango de operación seguro donde las llantas tienen buen agarre se indica en el recuadro rojo donde el máximo corresponde a un deslizamiento alrededor de 0.15 justo donde ocurren los picos máximos en el punto de mayor fricción. En este punto de la curva, el neumático es capaz de entregar hasta 5200 N. ¿Qué quiere decir esto? 5200 N de fuerza longitudinal tractiva de cada llanta corresponden a 10400 N en todo el eje, es decir la fuerza requerida para subir la pendiente es de 3700 N muy por abajo de la capacidad de las llanta, por ende se llega a la conclusión que las llantas son capaces realizar el trabajo que se les solicita.
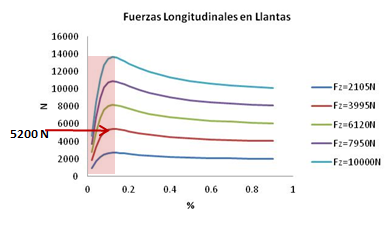
Figura 5. Curvas de fuerza deslizamiento longitudinales de llantas.