Este tema inicia con el análisis de correlación canónica, que se asemeja al análisis de correlación simple en el hecho de que busca encontrar relaciones entre variables. Sin embargo, este tipo de análisis va mucho más allá, tratando de predecir múltiples variables dependientes a partir de múltiples independientes, demostrando su validez.
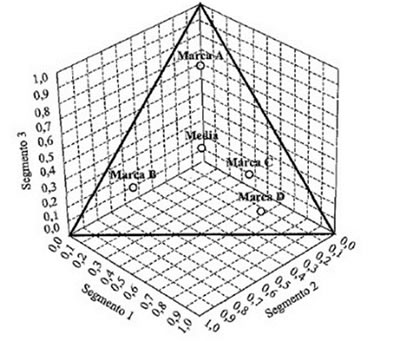
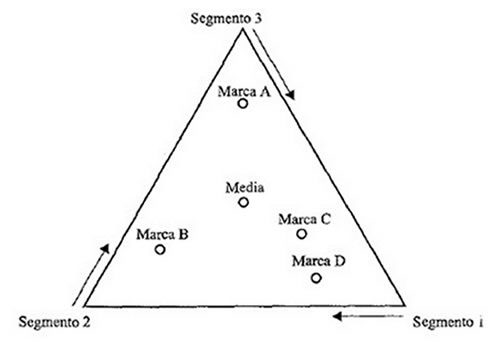
El análisis de correspondencias es una técnica muy utilizada entre los investigadores, sobre todo cuando se trata de posicionar marcas, productos o servicios, formas de distribución, etc.
Las principales aplicaciones al campo del marketing se pueden resumir en (Pérez, 2004; Luque, 2012):






9.1 Correlación canónica
Este tipo de análisis trata de sintetizar las relaciones existentes entre dos grupos de variables, evitando que en situaciones con muchas variables el análisis se reduzca al elemental estudio de las variables dos a dos (Luque, 2012).
Es una técnica útil y potente para explorar las relaciones entre variables dependientes e independientes múltiples. Es una técnica básicamente descriptiva, aunque puede ser usada para propósitos predictivos.
De acuerdo a lo marcado por Pérez (2004), el procedimiento es el siguiente:

9.2 Análisis de correspondencias

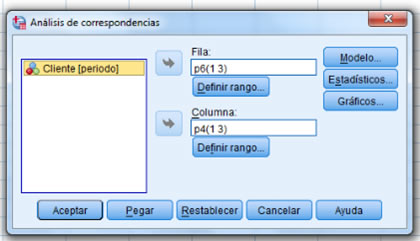
El análisis de correspondencias simple inicia con una tabla de contingencia de 2 variables, en la que cada casilla representa la frecuencia con la que se presenta. A partir de este punto, tiene una semejanza con el análisis de componentes principales, considerando a las filas como individuos y a las columnas como variables (Luque, 2012).
Este análisis trata de explicar la dispersión de la matriz de varianzas-covarianzas, ahora llamada matriz de inercia, a través de un número de variables o factores, realizando un análisis tanto para filas como para columnas. Dicho de otra forma, es como si se realizaran dos análisis de componentes principales, uno para el espacio definido por las filas y otro para el definido por las columnas.
Pérez (2004) nos hace una explicación del procedimiento, en el que partimos de una tabla de contingencia de I variables, con n categorías y J, con p, donde la intersección de una fila y una columna es la frecuencia con que se presenta la modalidad i de la variable I y la modalidad j de la variable J. A esta matriz de frecuencias se le llama matriz K.
Al no poder comparar los valores absolutos de dos filas o columnas, es necesario expresar la matriz K en términos relativos, dividiendo cada una de las frecuencias absolutas entre el total de las filas o columnas (k), para así obtener la matriz de frecuencias relativas (F).
Las distancias no se miden entre 2 filas o columnas, sino que se mide respecto del centro de gravedad definido a cada fila o columna. Este está definido por la masa de la columna (fj), mientras que para una columna es la masa de una fila (fi). Es un vector formado por puntos del tipo:
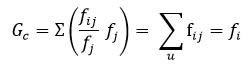
La distancia de una fila o columna hacia su centro de gravedad es su “media”. La dispersión o inercia de cada fila es la suma de las diferencias de cada punto respecto de su centro de gravedad ponderada por la masa de cada columna. Por tanto, la suma de la inercia de las filas es igual a la suma de la inercia de las columnas.
La inercia de una tabla es igual al estadístico x 2 y el número de individuos encuestados (k) es igual a cada uno de los sumandos en el cálculo de la inercia.
Una vez obtenidas las matrices de inercia para las columnas y filas, se procede a calcular los valores y vectores propios, y obtenemos las coordenadas estandarizadas de las filas y columnas (row and column profile). Otras formas de expresarlas es a través de la estandarización de las coordenadas de las columnas (column profiles), con la estandarización de las columnas (column profiles), o bien, con la estandarización canónica.
Si, por ejemplo, tenemos una tabla de contingencia representada por 3 factores, al tomarlo no perdemos información o inercia, representando de manera “perfecta” las filas o columnas.
Esto se demuestra con la siguiente expresión:
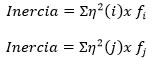
Donde 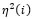 es la distancia de una fila al centro de coordenadas definido por los factores, y
es la distancia de una fila al centro de coordenadas definido por los factores, y 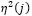 es la distancia de una columna al centro de coordenadas definido por los factores.
es la distancia de una columna al centro de coordenadas definido por los factores.
Ahora bien, si tomamos únicamente 2 factores, ya no se representa la totalidad de la inercia. Por ello, al cociente entre la inercia de cada fila, si se toma un número de factores menor y la inercia de cada fila —tomando todos los factores—, se conoce con el nombre de calidad de la representación de cada fila. Este cociente expresa la parte de la inercia de cada fila o columna que es explicada con los factores elegidos. De igual manera se hace con las columnas.
Las contribuciones sirven para interpretar los ejes. La contribución absoluta se define como la proporción de la inercia explicada por un factor debido a una fila o una columna. Para obtenerla se requiere calcular el autovalor asociado al factor 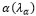 y la inercia explicada por una fila o una columna.
y la inercia explicada por una fila o una columna.
La contribución absoluta de una fila o columna es un porcentaje de la inercia que explica un factor, y la suma de las contribuciones para todas las filas o todas las columnas, en un determinado factor, debe ser 1, y depende no sólo de la distancia a la que se encuentre el punto, sino también de su peso o ponderación.
La contribución relativa expresa la contribución de un factor en la explicación de la fila o columna. Es la distancia que separa a una fila o columna en cada uno de los factores. Mide la calidad de representación de la fila o la columna sobre el factor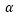
Para interpretar correctamente los ejes en un análisis de correspondencias es necesario identificar aquellas filas (o columnas) que mayor participación tienen en la formación del eje. Se examina así el conjunto de puntos que totalizan un determinado porcentaje en la formación del eje. Se busca aquellos puntos que están bien representados en los factores, es decir, aquéllos que tienen una alta contribución relativa, y se analizan sus coordenadas. La interpretación del factor se facilita cuando a los puntos con coordenadas positivas se opone puntos con coordenadas negativas.
Al igual que en el análisis factorial, es necesario definir el número de ejes. Hair (2007) indica que existen los siguientes criterios:
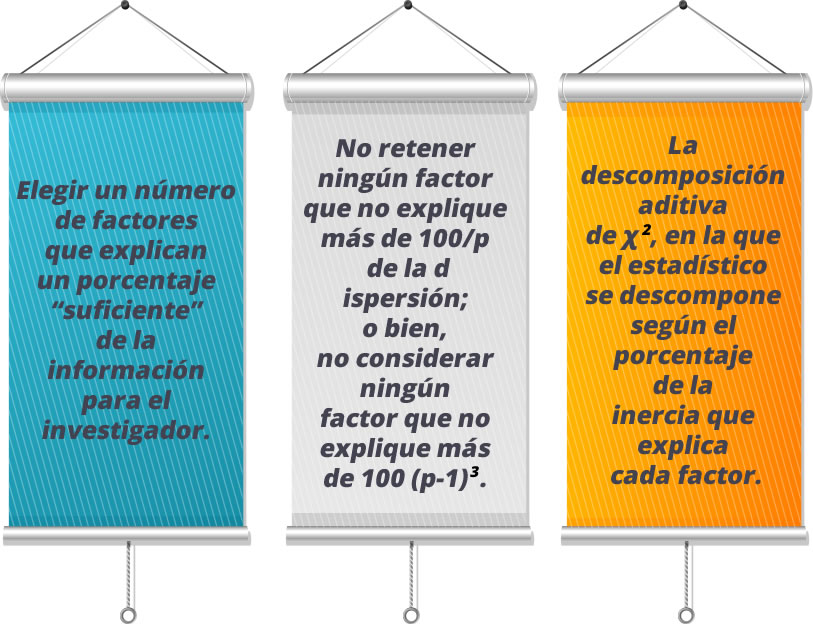
9.3 Análisis de correspondencias múltiples
En el punto anterior, el análisis se centró en una tabla bidimensional donde se cruzan 2 variables. Sin embargo, cuando el número de variables aumenta, es necesario realizar un análisis de correspondencias múltiple.
Este tipo de análisis requiere que los datos estén dispuestos en una tabla disyuntiva completa, en la que las filas están formadas por los individuos que han sido encuestados, y las columnas las categorías de las variables sometidas al análisis, de tal forma que cada celda está formada por 1, en el caso de que posea el atributo, y 0 en caso contrario (Hair, 2007).
El procedimiento es semejante al anterior y parte de la creación de la matriz o tabla disyuntiva completa.
Se calculan los centros de gravedad de cada inicial y columna, junto con la inercia. Al igual que antes, cuando una pregunta tiene un número de modalidades demasiado grande, la inercia debida a esta variable crece.
Se continúa diagonalizando la matriz para obtener autovalores y autovectores que permitan el cálculo de las coordenadas de las modalidades de las variables que están sometidas al análisis (Pérez, 2004).
La forma en que se examina la calidad de representación, así como la interpretación, es semejante al análisis de correspondencia simple.
9.4 Análisis factorial múltiple de tablas de contingencia
El método es un análisis en componentes principales ponderado que pretende representar una nube de puntos en un espacio de menor dimensión, donde se conserven de la mejor manera las distancias entre individuos.
Esto es semejante a buscar la menor dispersión o variabilidad en el espacio donde se proyecta la nube; es uno de los métodos estadísticos multivariantes con el que se puede analizar tablas de datos, la cual contiene Jc grupos o tablas de variables cuantitativas, Jq grupos o tablas de variables cualitativas (nominales) y los Jo grupos o tablas de variables cualitativas (ordinales) (Pérez, 2004).
El método se desarrolla en dos etapas:
1. Análisis separados
Se realiza un análisis de componentes principales para cada uno de los Jc grupos o tablas de variables cuantitativas, y realizar un análisis de correspondencias múltiples (ACM) para cada uno de los Jq grupos o tablas de variables cualitativas (nominales) y los Jo variables cualitativas (ordinales).
En el método AFM el tratamiento para los grupos o conjuntos de variables nominales y ordinales es el mismo.
En esta etapa se retiene en cada uno de los análisis, el mayor valor propio (llamado primer valor propio) denotado por λ j 1
2. Análisis global
Es un análisis de componentes principales (X, M, D) donde:
La matriz X es la matriz de datos transformados.
La matriz M es la matriz de métrica, y
La matriz D es la matriz de pesos.
Del análisis global ponderado, la matriz de métrica M, la matriz de pesos D y las coordenadas del individuo i sobre el primer eje factorial, se obtienen los valores de los primeros componentes principales.
Esta suma ponderada o combinación lineal obtenida se utiliza para construir un índice sintético.
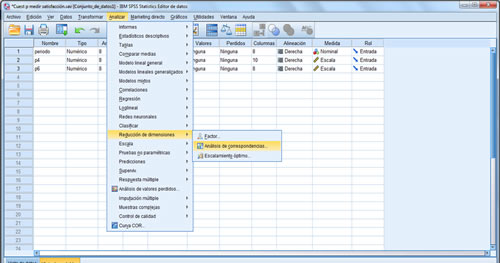
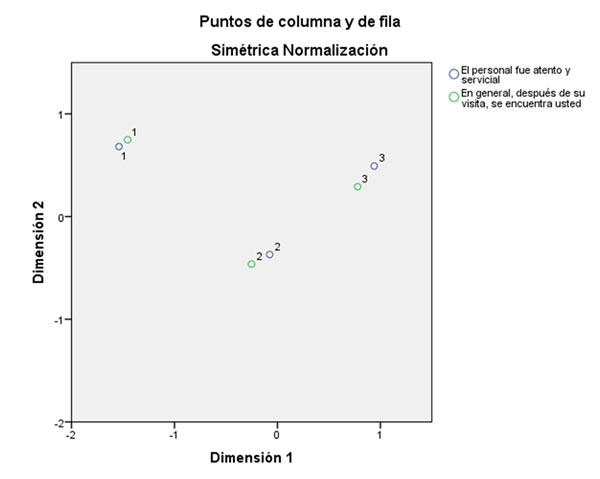
A continuación veremos un ejemplo de análisis de correspondencias y su interpretación.
Instrucciones: Haz clic para ver a detalle el ejemplo.

Revisa ahora un ejemplo sencillo siguiendo los pasos en PSPP, haciendo clic aquí.









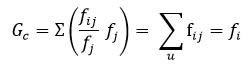
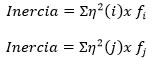
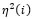 es la distancia de una fila al centro de coordenadas definido por los factores, y
es la distancia de una fila al centro de coordenadas definido por los factores, y 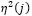 es la distancia de una columna al centro de coordenadas definido por los factores.
es la distancia de una columna al centro de coordenadas definido por los factores. 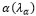 y la inercia explicada por una fila o una columna.
y la inercia explicada por una fila o una columna.