En el caso hipotético para identificar las razones por las cuales los consumidores compran una cierta marca particular de bebida (por ejemplo, Coca Cola). Se encontró la matriz de correlación, se encontraron los estadísticos descriptivos y los datos que indican correlación entre las variables mediante coeficientes de correlación, determinante, niveles de significación y análisis KMO, así como prueba de esfericidad de Bartlett.
El tipo de extracción que se sugirió fue el de componentes principales, en donde la varianza se toma como un todo, es decir, se supone que es explicable el 100% de la varianza, por lo cual se buscaron factores cuyo autovalor sea mayor a 1. Se optó también por realizar una rotación de factores Varimax, cuyos ejes son perpendiculares, y se pidió mostrar la solución rotada y los gráficos de saturación.
Los resultados obtenidos fueron los siguientes:
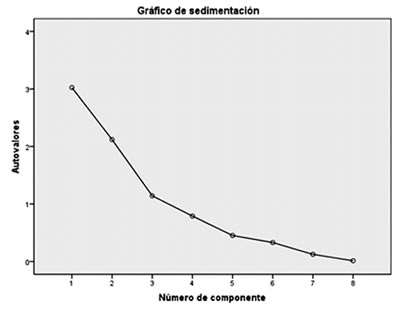
En el gráfico de sedimentación observamos que únicamente los componentes 1, 2 y 3 están en valores mayores o igual a 1, por lo cual tomaremos esos datos como representativos de nuestro análisis.
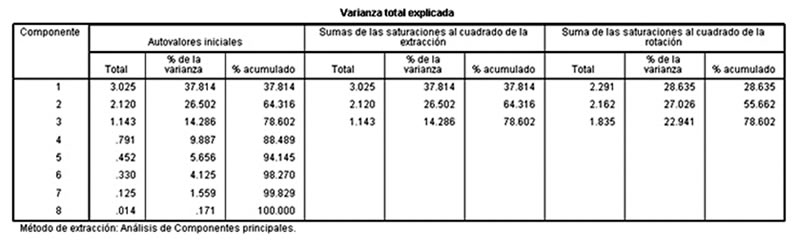
La tabla de varianza total explica a detalle la selección de esos tres componentes principales que contribuyen explicando el 78.602% de la varianza total, lo que significa que son representativos de los demás datos.
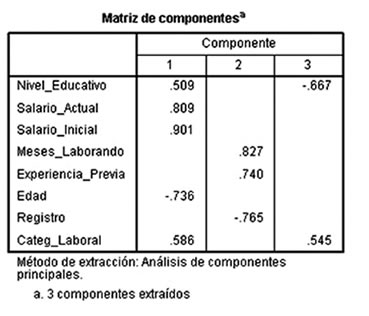
La matriz de componentes, matriz de factores o cargas factoriales sirve para explicar la correlación que existe entre cada variable y el componente en cuestión. Por ejemplo, para el componente 1 lo más importante es el salario inicial, el salario actual y la edad, aunque también toma en cuenta la categoría laboral y el nivel educativo. Para el componente 2 es más importante el número de meses laborando y la experiencia previa. Por último, el factor 3 involucra el nivel educativo y la categoría laboral. En este caso el primer componente abarca la mayoría de las variables.
Se procede ahora a analizar los valores rotados, a fin de quitar intercorrelaciones:

De igual forma, se puede observar que el primer factor está compuesto por tres variables: salario actual, salario inicial y categoría laboral; mientras que el segundo factor involucra el nivel educativo, los meses laborando y el registro. Asimismo, el tercer factor involucra el nivel educativo, la experiencia previa y la edad.
Aun cuando las cargas prevalecen en las mismas variables para los mismos factores, es mucho más clara la diferencia entre valores cercanos a 1 y valores cercanos a 0. Así, las variables asignadas a cada factor, a partir de la matriz de factores rotadas, son las mismas que se asignaron en la matriz de factores no rotados.
De esta forma hemos reducido ocho variables originales a sólo tres factores que representan tres bloques para el estudio de la percepción que tienen los consumidores sobre distintas cadenas de supermercados.
Así, los nuevos factores serán, Y1, Y2 y Y3, en donde:
Y1 corresponde a las variables agrupadas: X2 salario actual, X3 salario inicial, X8 categoría laboral.
Y2 corresponde a las variables agrupadas: X1 nivel educativo, X4 meses laborando y X7 registro.
Y3 corresponde a las variables agrupadas: X1 nivel educativo, X6 experiencia previa y X7 edad.







