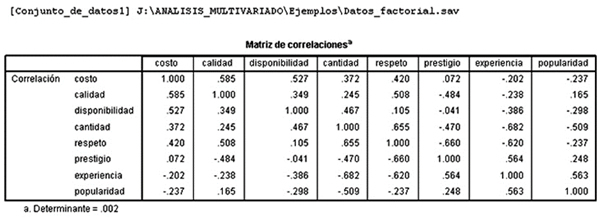
Contexto

El análisis factorial tiene su origen en la psicología, cuando Spearman (1863-1945) intentó analizar la inteligencia en los individuos, y propuso un factor general de inteligencia (llamado Factor G), que subyace a las habilidades para la ejecución de las tareas intelectuales. Según Spearman, una persona brillante sería buena  en cualquier área que intentara.

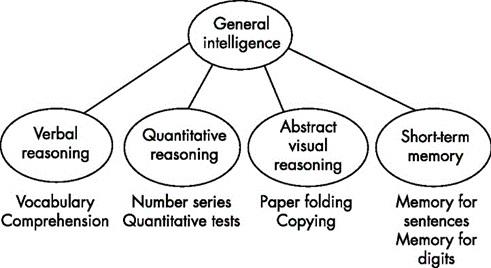
Imagen obtenida de https://chsappsych.wikispaces.com/Spearman,+Charles Sólo para fines educativos

Posteriormente, Thurstone mejoró el modelo explicando que la inteligencia tiene varios factores y que la inteligencia abarcaba al menos siete capacidades mentales: habilidad espacial, rapidez perceptual, habilidad numérica, significado verbal, memoria, fluidez verbal y razonamiento. De esta forma, se abre el panorama a la búsqueda de una variada serie de factores que pueden propiciar una determinada conducta.

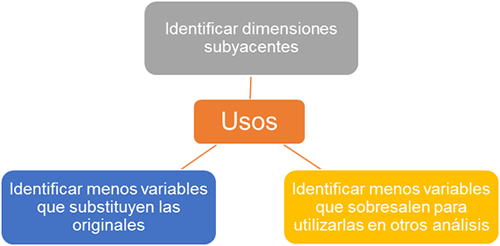
El análisis factorial es una técnica estadística de reducción de datos que se utiliza para explicar qué tanto varían las variables observadas en función de un número menor de variables llamadas factores.

En la actualidad, el análisis factorial se aplica a una gran cantidad de áreas como la economía, mediante la cual se realizan proyecciones para determinar índices de inflación y crecimiento en psicología en áreas del comportamiento, en estudios de mercado; para identificar la percepción que tienen los consumidores acerca de distintas cadenas de supermercados y en otras áreas como la medicina y la industria.

En adelante, te adentrarás en la técnica del análisis factorial, conocerás su aplicación, sus ventajas y desventajas, con el fin de que puedas utilizarla en cualquier situación que la necesites.

Preguntas detonadoras o de reflexión:

El análisis factorial se considera una técnica de interdependencia de variables:

  1. ¿Qué diferencias fundamentales piensas que existan entre los análisis con variables dependientes y los análisis con variables interdependientes?
  2. ¿Consideras que un análisis de este tipo podría tener más de una respuesta correcta?

Explicación

7.1 Conceptos y supuestos del análisis factorial

El análisis factorial es una técnica de las llamadas interdependientes que se utiliza para analizar variables interrelacionadas entre un gran número de variables, para explicarlas en términos de valores comunes llamados factores (Malhotra, 2008).

Un factor es un número que explica las correlaciones entre un conjunto de variables; por ejemplo, el factor que se interpreta como hombre hogareño se relaciona con un hombre responsable, bien conocido por la sociedad y hombre de familia.

Para poder aplicar la técnica multivariante de análisis factorial, se tienen que cumplir estos supuestos básicos:

Malhotra (2008) marca los siguientes supuestos básicos:

  1. Los factores pueden usarse para explicar la totalidad del problema.
  2. Las correlaciones que se observan entre las variables son el resultado del hecho de que tales variables comparten los mismos factores.
  3. La muestra presenta una distribución normal que se puede expresar como la combinación lineal de otros factores.

7.2 Objetivos de las técnicas de análisis factorial

El objetivo principal de un análisis factorial es encontrar la manera de condensar la información contenida en un número original de variables, en un número más pequeño de variables, sin perder información (Pérez, 2014; Malhotra, 2008; Hair, 2007).

Considera cuando se realiza una encuesta y se recoge un gran número de variables de forma simultánea (supón un cuestionario de satisfacción laboral), se necesita averiguar si las preguntas del cuestionario se agrupan de alguna manera característica. Al aplicar un análisis factorial a las respuestas se pueden encontrar grupos de variables con significado común y reducir el número de dimensiones necesarias para explicar las respuestas de los encuestados.

El análisis factorial también pretende reducir la dimensionalidad de datos, con el propósito de buscar el número mínimo de dimensiones capaces de explicar el máximo de información contenida en los datos. En este caso todas las variables cumplen el mismo papel, por lo que se elimina la dependencia/independencia de datos.

Una aplicación práctica del análisis factorial es mencionada por Malhotra (2008), quien afirma que —gracias a dicho análisis— la compañía bancaria JPMorgan Chase & Co logró identificar las dimensiones que usan los clientes para evaluar los bancos y desarrollar estrategias de marketing adecuadas; así, se convirtieron en el segundo banco más grande de Estados Unidos.

7.3 Clasificación de las técnicas de análisis factorial


Malhotra (2008) indica que el análisis factorial se utiliza en los siguientes casos:

  1. Para identificar las dimensiones subyacentes o factores que explican las correlaciones entre un grupo de variables.
  2. Para identificar un conjunto nuevo y más reducido de variables no correlacionadas que remplacen al conjunto original de variables correlacionadas en un análisis multivariado posterior.
  3. Identificar un conjunto más reducido de variables que sobresalen en un conjunto mayor para utilizar después en otro tipo de análisis multivariado.

Es de esperarse que, al eliminarse variables a criterio, los resultados finales varíen, si distintos investigadores aplican la técnica.

Así, el análisis factorial puede ser exploratorio o confirmatorio (Malhotra, 2008; Pérez, 2014): 

  • El análisis exploratorio se caracteriza porque no se conoce el número de factores, es empírico y el número de factores se determina durante la aplicación. Por ejemplo, una empresa que fabrica refrescos quiere incrementar sus ventas, por lo cual diseña una campaña de publicidad en donde aplica una encuesta para saber qué factores son más importantes para los consumidores, destacando: 
    1. Bebo refresco cuando estoy con amigos.
    2. Bebo refrescos sólo en ocasiones divertidas.
    3. En todos los sitios siempre pido el mismo refresco.
    4. Cambio de refresco constantemente porque me agrada cambiar de sabor.
    5. Sólo tomo refrescos cuando los mezclo con alcohol.
  • En el análisis confirmatorio los factores están fijados con anterioridad y se utilizan para su corroboración. A través del análisis confirmatorio se estudian los modelos de ecuaciones estructurales (éstas no se incluyen en el presente curso). Un ejemplo de análisis factorial en donde se aplica análisis confirmatorio es en la investigación en inteligencia; se sabe que aquellas personas que tienen nota alta en pruebas de habilidad verbal se desempeñarán bien en pruebas que requieran del uso de habilidades verbales y sólo por confirmar se hacen estas últimas pruebas.

El siguiente mapa mental muestra el algoritmo que se utiliza para llevar a cabo el análisis factorial exploratorio (recuerda que aquí no trabajaremos el análisis factorial confirmatorio) (Malhotra, 2008):

Algoritmos del análisis factorial (Malhotra, 2008)

Haz clic en cada dimensión para ver detalle:

Para revisar un ejemplo, haz clic aquí.

Cierre


Identificar las variables subyacentes en que se agrupan los clientes.


Los compradores de automóviles nuevos pueden agruparse de acuerdo al desempeño, a la economía o al lujo, lo cual da como resultado tres segmentos de compradores: buscadores de desempeño, buscadores de economía o buscadores de lujo.


Cuando se investiga un producto sirve para determinar los atributos de la marca que influyen en el consumidor.


En situaciones de calidad del agua se utiliza el análisis factorial para determinar qué elementos son predominantes en algún tipo de contaminación.


El análisis factorial se emplea en estudio de asignación de precios para identificar las características de los consumidores sensibles a los precios.

El siguiente paso será resolver problemas que sean candidatos para aplicar esta técnica multivariante. Estás a un paso de encontrar el cómo del análisis factorial.

Es recomendable el uso de un paquete estadístico (PSPP, XSTAT o Minitab), para hacer el trabajo con los datos de forma eficiente. Existen versiones de prueba y versiones para estudiantes. Para ello puedes consultar: http://pspp.awardspace.com/ o http://www.xlstat.com/. El primero es un paquete estadístico de mucha tradición y el segundo son applets de Excel.

¿En qué casos consideras que pueda ser útil para una empresa reducir el número de factores o variables en un análisis?

Checkpoint

Antes de concluir el tema, asegúrate de poder contestar las preguntas que se enlistan a continuación.

Instrucciones: Haz clic en cada pregunta para conocer su respuesta.

El uso más común del análisis factorial es para reducir un determinado número de variables en un conjunto más pequeño, más sencillo de manejar y que logra explicar una buena proporción de las variables originales. Estas nuevas variables, llamadas factores o componentes, pueden ser útiles en dos formas: para substituir las variables originales y para ser utilizadas en otros tipos de análisis multivariados.

Otro uso común es el hecho de encontrar factores o dimensiones subyacentes, que no son perceptibles a simple vista, pero que sirven para explicar las correlaciones entre un grupo de variables.

Los eignevalues o autovalores indican la cantidad total de varianza que un factor en particular está explicando. Dicho de otra forma, un eigenvalue equivale a la suma de los cuadrados de los pesos por columna en una matriz factorial.

Entre más elevado sea el eigenvalue, más elevada será la explicación que éste da (respecto de la varianza), más importante es y, por lo tanto, más variables estará agrupando.

Un criterio común es no considerar factores cuyo autovalor sea inferior a 1. Esto se debe a que el valor máximo que una carga factorial puede tener es precisamente 1. Si el eigenvalue es inferior a ese valor, su importancia será igual o menor que la de cualquier variable. De hecho, podemos decir que estará resumiendo una cantidad mínima de la varianza y, por lo tanto, no es de mucha utilidad.

Referencias

Libro de texto:

  • Malhotra, N. (2008). Investigación de Mercados: Un enfoque aplicado. (5ª ed.) México: Pearson. 
    ISBN: 9789702611851

Libros de apoyo:

  • Malhotra, N. (2008). Investigación de Mercados: Un enfoque aplicado. (5ª ed.) México: Pearson. 
    ISBN: 9789702611851
  • Pérez, L.C. (2014). Técnicas de Análisis Multivariante de Datos. España: Pearson /Prentice Hall. ISBN: 9788483229019

Glosario

Cargas de los factores: son correlaciones simples entre las variables y los factores.

Gráfica de sedimentación: es una gráfica de los valores propios contra el número de factores en orden de extracción.

Eeigenvalue (autovalor o valor propio): representa la varianza total explicada por cada factor.

Índice de Kaiser-Meyer_Olkin (KMO): indicador que sirve para examinar si el análisis factorial es adecuado. Valores altos (entre 0.5 y 1.0) indican que sí es adecuado, mientras que valores menores a 0.5 implican que el análisis factorial tal vez no sea adecuado. 

Matriz de correlación: es una matriz triangular inferior que muestra las correlaciones simples entre pares posibles de variables incluidas en el análisis. Los elementos de la diagonal tendrán valores iguales a 1.

Matriz factorial: contiene cargas de los factores de todas las variables en todos los factores derivados. 

Puntuaciones de los factores: son calificaciones compuestas que se calculan para cada encuestado en los valores residuales.

Prueba de esfericidad de Bartlett: es una prueba estadística que se utiliza para examinar la hipótesis de que las variables no están correlacionadas en la población. En otras palabras, la matriz de correlación de la población es una matriz de identidad; cada variable tiene una correlación perfecta consigo misma, pero no tiene correlación con las demás.

Residuales: son las diferencias entre las correlaciones observadas (tal como se presentan en la matriz de correlaciones de entrada) y las correlaciones reproducidas (como se calcularon en la matriz factorial).