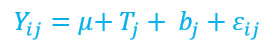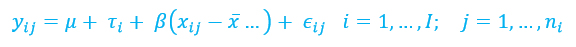6.1 Diseño de bloques al azar
De acuerdo a Hair (2007), en estadística, se conoce como bloque a un grupo de observaciones que tienen condición de unicidad estadística, es decir, pueden ser analizadas e interpretadas sólo de modo conjunto.
En general, un bloque puede estar fijado o establecido por el investigador de forma arbitraria. En ese caso, se dice que el bloque es no aleatorio. Cuando un bloque está fijado, configurado y seleccionado al azar se dice que el bloque es un bloque aleatorio.
El diseño de bloque aleatorizado representa una alternativa al ANOVA y al ANCOVA. Se somete a los sujetos a medidas que implican un efecto adicional (los bloques), y se les agrupa de acuerdo con sus puntuaciones. Los grupos de sujetos se convierten en los niveles de las variables independientes de interés en el diseño factorial (Malhotra, 2008). La interpretación del efecto principal de las variables independientes es directa. En el caso de la ANCOVA (análisis de covarianza) se elimina la variación debida a las covariables de la estimación de la varianza del error y se le evalúa como un efecto principal separado (Pérez 2014; Malhotra, 2008).
Es importante tomar en cuenta que la característica por la cual se hace el bloqueo no es la característica que interesa evaluar, sino que —al tener una variable que sospechamos puede influenciar la variable respuesta— si queremos eliminar su efecto, la involucramos en el modelo.
Ventajas y desventajas del diseño de bloques completos al azar
- Aumenta la potencia de la prueba porque la variabilidad atribuible a la heterogeneidad de las unidades experimentales es extraída del error experimental.
- Hay cierta flexibilidad, pues no hay restricciones en el número de tratamientos o de bloques.
- Al evaluar los tratamientos bajo diferentes condiciones se amplía la base inferencial del experimento.
- Puede ser muy difícil conseguir bloques homogéneos.
- El diseño de bloques aleatorizado no es adecuado si existe interacción entre los bloques y los tratamientos, es decir, si los efectos de tales factores no son aditivos.
Pérez (2014) y Hair (2007) indican la forma de construir un modelo lineal:
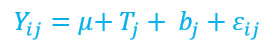
Donde:
Yij es la lectura del tratamiento i-ésimo en el j –ésimo bloque.
μ es el promedio poblacional de la variable respuesta.
Tj es el efecto del tratamiento ‘i’ con i = 1, 2, …., t.
bj es el efecto del bloque j con j = 1, 2, …. R.
εij es el efecto asociado con la lectura del í-esimo tratamiento en el j-ésimo bloque.
Fórmulas del diseño de bloques al azar
| F de V |
GL |
Suma de cuadrados |
Cuadrados medios |
FC |
| Tratamientos |
t – 1 |
T=ΣYi2 / (r-TC) |
SC T=T / (t-1) |
|
| Bloques |
r – 1 |
B = ΣYj2 / (t-TC) |
SCF = B / (r-1) |
|
| Error |
(t -1)(r-1) |
E = Tot - T - B |
SCF = E / (t-1) (r-1) |
|
| Total |
n – 1 |
Tot = ΣΣYij2 - TC |
|
|
Donde:
F de V: Fuente de Variación. TC: Término de corrección = Y2.. /n .
GL: Grados de libertad. Yi: Total del tratamiento ‘i’.
t: Número de tratamientos. Yj: Total del bloque ‘j’ .
r: Número de bloques.
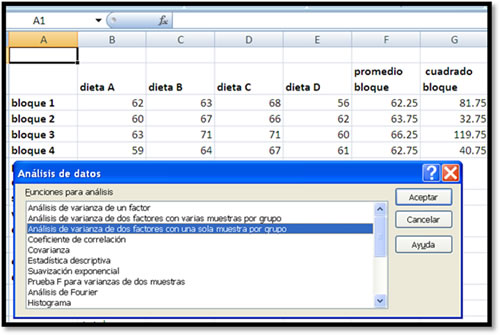
El análisis se puede resolver en Excel, simplemente encontrando la suma de cuadrados y los cuadrados medios, como se realizó en el análisis de varianza o se puede utilizar Excel en Datos/Análisis de datos/ Análisis de varianza de dos factores con una sola muestra por grupo (Malhotra, 2008).
Para revisar un ejemplo, haz clic aquí.
6.2 Análisis de covarianza
Al examinar las diferencias entre las medias de la variable dependiente relacionadas con el efecto de las variables independientes controladas, muchas veces es necesario tomar en cuenta la influencia de las variables independientes no controladas.
Malhotra (2008) dice que el análisis de covarianza es una combinación de dos técnicas:
En el análisis de covarianza:
- La variable respuesta es cuantitativa.
- Las variables independientes son cualitativas y cuantitativas.
Por ejemplo:
- Determinar la variación de las intenciones de compra de una marca en los consumidores con diferentes niveles de precio, es posible que se necesite tomar en cuenta la actitud hacia la marca.
- Al determinar cómo evalúan una marca distintos grupos expuestos a comerciales diferentes, es probable que sea necesario controlar los conocimientos previos.
- Al determinar la manera en que los distintos niveles de precio afectarán el consumo de cereal de una familia, quizá sea necesario tomar en cuenta el tamaño de ésta.
En estos casos es útil usar el análisis de covarianza
Al igual que en el análisis de regresión existen distintos análisis de covarianza (Unifactorial y Multifactorial); para este curso usaremos sólo el análisis Unifactorial.
Covarianza Unifactorial. La respuesta Y está relacionada con una variable cualitativa t y una o más variables cuantitativas X (Pérez, 2014; Malhotra, 2008; Hair, 2007).
- La variable cualitativa t recibe el nombre de factor.
- La variable cuantitativa X recibe el nombre de covariable o variable concomitante.
La covariable es usada para eliminar variaciones extrañas de la variable dependiente, ya que los efectos de los factores son muy importantes. La variación de la variable dependiente, debido a las covariables, se elimina mediante un ajuste del valor promedio de la variable dependiente dentro de cada tratamiento y después se realiza un análisis de varianza con las puntuaciones ajustadas. El nivel de significancia del efecto combinado de las covariables, así como del efecto de cada covariable, se prueba con el estadístico F adecuado (Malhotra 2008).
Pérez (2014) y Malhotra (2008) refieren que el modelo unifactorial con una covariable cumple la siguiente fórmula:
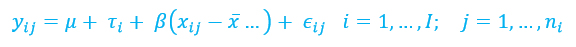
Donde:
τi representa el efecto producido por el tratamiento i- ésimo.
B representa el coeficiente de regresión lineal.
xij representa el valor de la covariable correspondiente a la observación yij .
x representa la media de la covariable.
Eij representa el error aleatorio.
En un diseño aleatorizado, la suma total de cuadrados puede descomponerse en suma de cuadrados entre tratamientos y en suma de cuadrados residual (de forma semejante al análisis de varianza).
Ejemplo:
Haz clic en la imagen para ver el ejemplo.

Finalmente, dentro de la interpretación de la ANOVA, un aspecto importante en el análisis de varianza muchas veces es el de las interacciones. Las interacciones surgen al realizar un ANOVA de dos o más factores. Si en el resultado ANOVA obtenemos que no hay interacción, significa que las interacciones no son significativas. Un efecto de interacción ocurre cuando el efecto de una variable independiente, sobre una variable dependiente, difiere para las distintas categorías o niveles de otra variable independiente. El ANCOVA puede servir para minimizar esas interacciones al corregir el modelo.