En la mayoría de las situaciones que analizamos deseamos conocer si existen diferencias entre un par de muestras, pero influye más de un factor en su determinación.
5.1 Análisis de varianza de un factor y pruebas de comparación múltiple
En el tema anterior, se trabajó con el análisis de varianza de un factor y se explicaron sus supuestos, sus objetivos y la forma de resolverlo. Definimos el análisis de varianza de un factor como la técnica ANOVA en la cual sólo influye un factor. El ANOVA es la técnica estadística que sirve para examinar las diferencias entre las medias de dos o más poblaciones.
Pruebas de comparación múltiple
Para evaluar si existe diferencia entre varias poblaciones, en donde sólo tenemos un factor, tuvimos que seguir cierto procedimiento (Malhotra, 2008):

- Identificación de las variables dependiente e independiente. Por convención se denomina Y a la variable dependiente y X a la variable independiente con c categorías, y en el experimento para cada valor de X existe un valor Y a analizar con n observaciones de Y.
- Descomposición de la varianza total. La varianza total se descompone en SCentre y scintra, donde SCentre es la variación en las medias de las categorías de X. En el caso de SCintra no está explicada por X y, por tanto, se conoce como SCerror.
- Medición de los efectos. Los efectos de X sobre Y se miden con SCentre porque este valor está relacionado con la variación de las medias de las categorías de X, la magnitud relativa de SCentre aumenta conforme aumentan las diferencias entre las medias de Y en las categorías de X.
- Prueba de la significancia. En el análisis de varianza de un factor, el interés reside en poner a prueba la hipótesis nula que plantea que las medias de las categorías son iguales en la población, o sea: µ1 =µ2 = µ3= … = µc. La hipótesis nula se prueba con el estadístico F, tomando en cuenta la proporción entre los cuadrados medios CM:
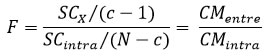
El estadístico F con (c-1) y (N-c) grados de libertad que se busca en tablas para determinar si está en el nivel de confianza.
- Interpretación de los resultados. Si la hipótesis nula no se rechaza, la variable independiente no tiene un efecto significativo sobre la variable dependiente; en cambio, si la hipótesis nula se rechaza, el efecto de la variable independiente es significativo.
5.2 Análisis de varianza con dos factores con interacción
En la investigación de mercados frecuentemente necesitamos conocer el efecto de más de un factor al mismo tiempo como puede ser (Malhotra, 2008):
- ¿Cómo varían las intenciones de los consumidores al comprar determinada marca, de acuerdo a distintos niveles de precios y presentación?
- ¿De qué forma interactúan los niveles de publicidad para afectar las ventas de una marca?
- ¿Cómo afecta al consumo de determinada marca la preparación del consumidor y su edad al mismo tiempo?
- ¿Qué efecto tiene la familiaridad del consumidor y la imagen de la tienda sobre su preferencia de consumo en la misma?
Para poder determinar este tipo de efectos, se puede emplear un análisis de varianza de n factores. Una de las principales ventajas de esta técnica es que permite al investigador examinar interacciones entre los factores. Las interacciones ocurren cuando los efectos de un factor sobre la variable dependiente dependen del nivel (categoría) de los otros factores. El procedimiento para realizar el análisis de varianza de n factores es similar al del análisis de varianza de un factor. Los estadísticos asociados con el análisis de varianza de n factores también se definen de forma similar (Pérez, 2014; Malhotra, 2008).
En este caso, la variación total se descompone de la siguiente manera:
SCtotal = SC debida a X1 + SC debida a X2+ SC debida a la interacción de X1 y X2 + SCintra o
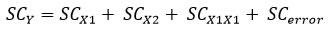
Un mayor efecto de X1 se reflejará en una mayor diferencia promedio en los niveles de X1 y en una SCX1 más grande. Lo mismo ocurre con el efecto X2. Cuanto más grande sea la interacción entre X1 y X2, mayor será SCX1X2. Si X1 y X2 son independientes, SCX1X2 tendrá valores cercanos a cero.
La fuerza del efecto llamado efecto general o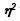 múltiple se define como:
múltiple se define como:
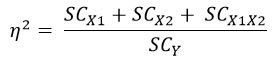
En este caso, la significancia del efecto general se prueba con una prueba F:
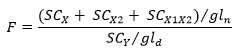
Con gln grados de libertad del numerador y gld grados de libertad del denominador que están definidos por:
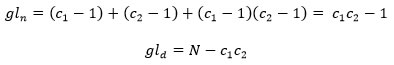
Si el efecto general es significativo, conviene examinar la significancia del efecto de la interacción(Pérez, 2014). El análisis es muy similar al anterior:
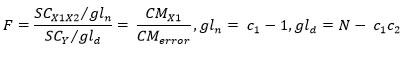
Ejemplo
En unas pruebas que se desarrollaron para evaluar vacunas se utilizaron tres concentraciones de determinado suero. Se midió el porcentaje de eficiencia de la vacuna y se realizó un experimento en cuatro bloques para evaluar el comportamiento de las vacunas:
| |
250gr/lt |
215gr/lt |
143gr/lt |
Testigo |
| Bloque I |
49.86 |
45.59 |
0.59 |
46.18 |
| Bloque II |
45.25 |
49.21 |
50.12 |
49.86 |
| Bloque III |
56.22 |
45.12 |
49.87 |
48.16 |
| Bloque IV |
47.37 |
46.14 |
49.02 |
44.73 |
Se plantea la hipótesis:
Ho: todas las concentraciones del suero producen el mismo efecto.
Ha: al menos una de las concentraciones del suero produce un efecto distinto.
Para resolver el Excel, se capturan todos los datos y se procede de la siguiente manera:
Se selecciona: Datos / Análisis de datos / Análisis de varianza de dos factores con una sola muestra por grupo / Aceptar.
Como en el caso del Análisis de varianza de un factor se seleccionan los datos en los cuadros de diálogo en cuanto a rango de entrada, nivel de significancia y rango de salida.
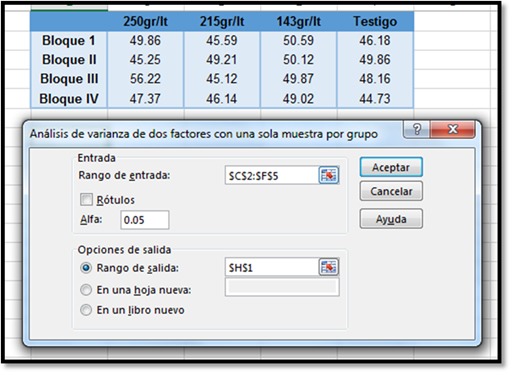
Interpretación de resultados
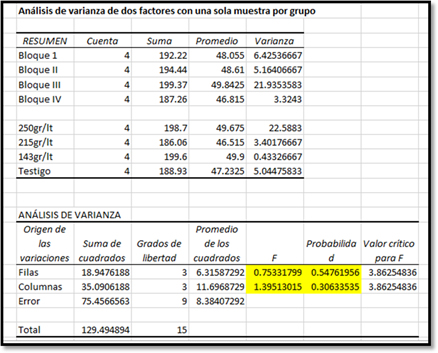
Podemos observar que el valor calculado de F fue de 1.395, que resulta inferior al valor crítico de 3.86 (llamado valor tabular), que da un valor-p = 0.306 con un nivel de significancia del 0.05.
En el caso de F para bloque es de 0.75, que resulta ser inferior al valor crítico de 3.86, lo cual es equivalente a analizar su valor-p correspondiente de 0.54 con un nivel de significancia de 0.05.
De acuerdo a los resultados, se puede afirmar que no hay diferencia en el efecto de las tres concentraciones de la vacuna. Tampoco hay diferencia entre aplicar o no la vacuna, puesto que no hay diferencia con el testigo tampoco.



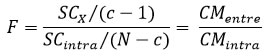
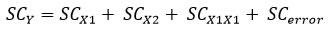
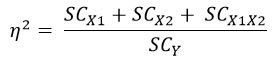
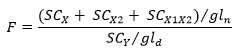
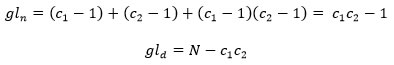
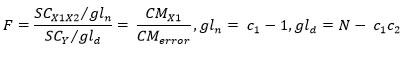


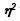 ): la fuerza del efecto conjunto de dos o más factores o el efecto general.
): la fuerza del efecto conjunto de dos o más factores o el efecto general.