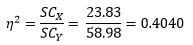4.1 Conceptos y supuestos básicos
¿Existe alguna diferencia, a simple vista, en los morteros presentados arriba? Recuerda que para que dos productos sean iguales deberán tener características similares tanto en material, tamaño, marca, forma etc.
El análisis de varianza sirve para determinar si dos morteros de diferentes lotes son iguales o diferentes.
Tanto el análisis de varianza, como el análisis de covarianza, se utilizan para examinar las diferencias entre los valores promedio de la variable dependiente, asociada con el efecto de las variables independientes controladas, después de tomar en cuenta la influencia de las variables independientes no controladas. El análisis de varianza ANOVA se usa como una prueba de medias para dos o más poblaciones (Pérez, 2014).
La hipótesis nula generalmente plantea que todas las medias son iguales.
Supuestos del análisis de varianza (Malhotra, 2008):
- La variable dependiente debe medirse al menos a nivel de intervalo.
- La distribución de residuos debe presentar una distribución normal.
- Debe existir homocedasticidad, esto es, homogeneidad de las varianzas.
4.2 Clasificación de las técnicas del análisis de varianza
Existen distintos tipos de pruebas que forman parte del análisis de varianza:
4.3 Objetivos de las técnicas del análisis de varianza
- Analizar la diferencia entre grupos a través de parámetros como la media.
- Comparar los errores sistemáticos con los aleatorios obtenidos al realizar diversos análisis en cada experimento.
Acorde a Malhotra (2008), el procedimiento para elaborar el análisis de varianza de un factor es el siguiente:
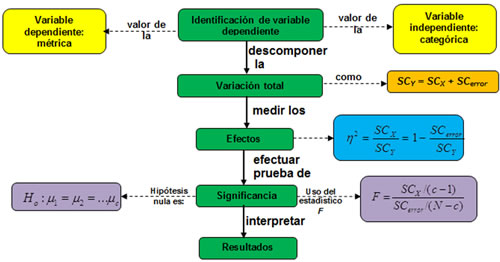
Instrucciones: Haz clic en cada dimensión para ver el detalle
La variable dependiente se simboliza con la Y ,mientras que la independiente se simboliza con la X. Existen n observaciones de Y para cada categoría de X, de tal forma que el tamaño de la muestra en cada categoría de X es n y el tamaño total de la muestra será N = n x c.
El análisis de varianza recibe su nombre porque examina la variabilidad o variación en la muestra (variable dependiente) y con base en la variación determina si hay alguna razón para creer que las medias poblacionales son diferentes.
La manera gráfica de visualizar la descomposición de la variación total ANOVA de un factor es la siguiente:
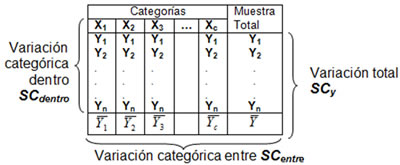
La variación total en Y es descrita como SCY = SCentre + SCdentro , donde los subíndices entre y dentro se refieren a las categorías de X. SCentre es la variación entre las categorías de X, o sea, es la porción de la suma de cuadrados en Y relacionada con la variable independiente o factor X . Por eso también se describe como SCX . La SCdentro no puede explicarse por X, por lo que se le conoce como SCerror. La variación total en Y, por tanto, se descompone de la siguiente manera:
SCY = SCX + SC error
En donde:
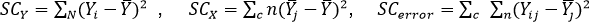
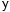
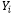= observación individual
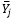= media de la categoría j
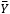= media de la muestra total o gran media
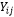= i-ésima observación en la categoría j-ésima
En el análisis de varianza se calculan dos medidas de variación: dentro de los grupos SCdentro y entre grupos SCentre. La variación dentro de los grupos es una medida de cuánto varían, dentro de un grupo, las observaciones o valores de Y. Esto se utiliza para estimar la varianza dentro de un grupo en la población. Se supone que todos los grupos tienen la misma variación en la población, sin embargo, no se sabe si todos los grupos tienen la misma media, por eso no se puede calcular la varianza de todas las observaciones en conjunto. De forma similar se puede obtener otro estimado de la varianza de los valores de Y al examinar las variaciones entre las medias muestrales y el tamaño de los grupos de muestras para estimar la varianza de Y.
Si la hipótesis nula es verdadera y las medias de la población son iguales, la estimación de la varianza basada en la variación entre grupos es correcta. Si los grupos tienen medias diferentes en la población, la estimación de la varianza, basada en la variación entre grupos, será demasiado grande. Así pues, al comparar los estimados de la varianza de Y con base en la variación entre grupos y dentro de grupos se pone a prueba la hipótesis nula.
Los efectos de X sobre Y se miden con SCX. Como SCX está relacionada con la variación en las medias de las categorías de X, la magnitud relativa de SCX aumenta conforme aumentan las diferencias entre las medias de Y en las categorías de X. La magnitud relativa de SCX también aumenta cuando las variaciones en Y, dentro de las categorías de X, disminuyen. La fuerza de los efectos de X sobre Y se miden de la siguiente forma:
El valor de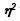
varía entre 0 y 1 y valdrá cero cuando todas las medias de la categoría sean iguales, indicando que X no tiene efecto sobre la Y. El valor de 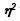es una medida de la variación en Y que está explicada por la variable independiente X.
En el análisis de varianza de un factor lo que se pretende es probar la hipótesis nula que plantea que las medias de las categorías son iguales en la población, o sea
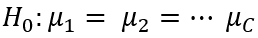
De acuerdo con la hipótesis nula, SCX y SCerror provienen de la misma fuente de variación. En tal caso, el estimado de la varianza poblacional de Y se puede basar en la variación de la categoría entre o en la variación de la categoría dentro. De tal forma que se obtiene:
La hipótesis nula se prueba con el estadístico F, con base en la proporción entre los dos estimados:
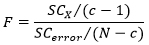
En donde (c – 1) representa el numerador y (N – c) representa los grados de libertad.
Si la hipótesis nula no se rechaza, entonces la variable independiente no tiene un error significativo sobre la variable dependiente. Si se rechaza la hipótesis nula, entonces el efecto de la variable independiente es significativo.
EJEMPLOS
Ejemplo 1:
Se forman tres grupos de 6 alumnos que estudian en distinta modalidad: presencial, ejecutiva y en línea. Los datos del examen son los siguientes:
| Presencial |
4.8 |
7.1 |
5.4 |
6.8 |
8.6 |
6.2 |
| Ejecutiva |
4.9 |
6.1 |
5.4 |
3.6 |
4.2 |
2.4 |
| En línea |
1.5 |
6.5 |
3.9 |
5.3 |
2.4 |
3.1 |
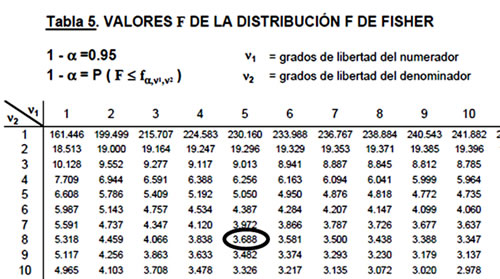
Realizar el ANOVA con α = 0.05
Hay 3 grupos (c = 3), cada uno con 6 datos, (n = 6) por lo que N = 18.
La suma de cada grupo es la siguiente: Sp = 38.9, Sej = 26.6, Sel = 22.7, Total: 88.2
- Plantear hipótesis nula:
Ho: µ1 = µ2 = µ3
H1: µi ≠ µ2 al menos una µ es diferente.
- Cálculo de SCXy SCerror.
SCx = 6 (6.48333 – 4.9)2 + 6 (4.4333 – 4.9)2 + 6 (3.78333 – 4.9)2 = 23.83
SCerror = (4.8 – 6.4833)2 + (7.1 – 6.4833)2 + (5.4 – 6.4833)2 + … (4.9 – 4.333)2 + (6.1 – 4.333)2 + (5.4-4.333)2 + … + (1.5 – 3.7833)2 + (6.5 – 3.7833)2 + (3.9 – 3.7833)2 + … = 35.15
SCY = SCX + SCerror = 23.83 + 35.15 = 58.98
Para calcular los efectos:
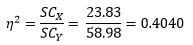
Y finalmente el estadístico F:
Como el valor de F es mayor a 3.68 se rechaza la hipótesis nula, lo que significa que no todas las medias poblacionales son iguales aun cuando no no se sabe en dónde están las diferencias. Es posible identificar la relación entre las distintas modalidades haciendo la matriz de correlación, con lo cual se identifica que las modalidades con menos relación son la presencial – ejecutiva, con un índice de correlación de -0.11. Esto quiere decir que las modalidades no presentan ningún tipo de correlación.
| |
Presencial |
Ejecutiva |
En línea |
| Presencial |
1 |
-0.11048824 |
0.25092169 |
| Ejecutiva |
-0.11048824 |
1 |
0.32594127 |
| En línea |
0.25092169 |
0.32594127 |
1 |
Ejemplo 2:
Para resolver el ejemplo, utilizaremos Excel y explicaremos cómo aplicarlo.
En un estudio realizado por estudiantes de Agronomía, se evaluaron 4 fungicidas para proteger semillas de soya. Los productos se aplicaron en lotes de semilla. De cada lote se extrajeron 5 muestras al azar (cada una con 100 semillas), y se pusieron a germinar junto con otra muestra que no tenía ningún tratamiento. Los resultados son los siguientes:
| Porcentaje de semillas germinadas en la muestra. |
| Sin tratamiento |
Fungicida 1 |
Fungicida 2 |
Fungicida 3 |
Fungicida 4 |
| 90 |
94 |
90 |
91 |
91 |
| 90 |
94 |
91 |
92 |
93 |
| 91 |
96 |
92 |
91 |
95 |
| 92 |
91 |
95 |
96 |
95 |
| 92 |
95 |
90 |
90 |
94 |
- Plantear la hipótesis:
Ho: todos los fungicidas producen el mismo efecto sobre la protección de semillas de soya a nivel de germinación.
H1: al menos uno de los productos produce un efecto distinto sobre la protección de semillas de soya a nivel de germinación.
- Se selecciona la prueba a realizar en Excel para hacer el análisis: Datos/Análisis de Datos/ Análisis de varianza de un factor.
Los resultados que presenta Excel son los siguientes:
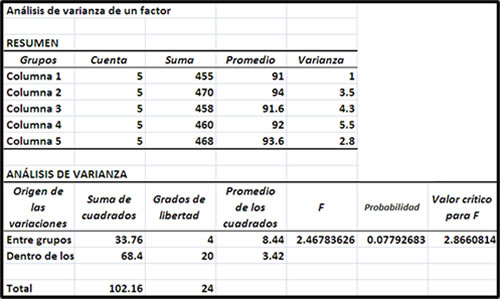
Se observa que los primeros datos presentados son el promedio y la varianza de cada una de las muestras.
El valor calculado del estadístico F es de 2.46 que resulta inferior al valor de tablas de F de 2.86 (se toma como numerador el gl entre grupos, que es 4, y como denominador el gl dentro que es 20).
El valor de p es de 0.0779.
De acuerdo a los resultados, podemos decir que no hay evidencia suficiente para rechazar la hipótesis nula (Fc < Ftab o p > 0.05), por lo cual podemos decir que no hay diferencia entre los cuatro productos utilizados, incluso no hay diferencia entre el uso o no de producto para proteger de la germinación de las semillas.
Observa que, como el análisis de Excel presentó los valores de Fque da significancia a la prueba, ya no es necesario encontrar.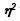
