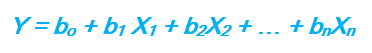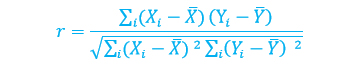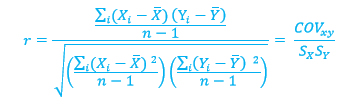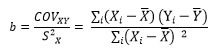Contexto

Habrá alguna relación entre la cantidad de cigarros que una persona fume al día y el estado de salud que presente?

Aun cuando la respuesta es obvia y nada extraña (actualmente se sabe que sí existe una relación directa entre el estado de salud de una persona y la cantidad de cigarros que fuma al día), cuando se quiere dar una respuesta científica al hecho es necesario presentar evidencias numéricas que lo sustenten.

El tema de regresión se estudió de manera breve durante el módulo anterior, partiendo del concepto de correlación. Ahí aprendiste a identificar si existía alguna relación entre parámetros y qué tipo de relación era ésta.

En este tema estudiarás a profundidad la correlación y regresión utilizando esos datos para realizar pronósticos útiles en la toma de decisiones.

Preguntas detonadoras o de reflexión:

¿Qué podría ocurrir si la variable de interés no está correlacionada con la variable independiente?

¿Piensas que sólo las variables métricas son útiles para hacer predicciones?

Explicación

3.1 Definición

El análisis de regresión es una técnica estadística que tiene como objetivo establecer modelos matemáticos para representar, formalmente, las relaciones de dependencia existentes entre un conjunto de variables estadísticas (Malhotra, 2008; Pérez, 2014).

“En el análisis denominado regresión simple están involucradas dos variables: una independiente y otra dependiente únicamente; mientras que en el análisis denominado regresión múltiple están involucradas más de dos variables independientes y una sola variable dependiente.”


3.2 Objetivos de la regresión múltiple

El objetivo del análisis de regresión es encontrar la relación (generalmente lineal) entre una variable dependiente o de criterio Y y otra variable independiente o predictora denominada X . 

Si el caso es de regresión múltiple estarán involucradas más de dos variables en donde existirá una variable dependiente o de criterio Y y variables independientes o predictoras X1, X2, …., Xk, con las cuales construiremos una ecuación (generalmente lineal) para predecir resultados.

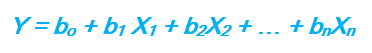
3.3 Supuestos en el análisis de regresión múltiple

Malhotra (2008) marca los supuestos que debe cumplir cualquier conjunto de datos al que se desea aplicar análisis de regresión, sea simple o múltiple, son los siguientes:

Normalidad

    • Es decir, para cada valor de Xi habrá una respuesta Y que cumplirá con tener una distribución normal.

Linealidad

    • Es decir, que la Y puede expresarse como una combinación lineal de Xi

Homoscedasticidad

    • Es decir, la variabilidad de Y que es la medida de su varianza (s2) o su desviación estándar (s) debe ser la misma para cada valor Xij de su variable Xi.

Regresión simple

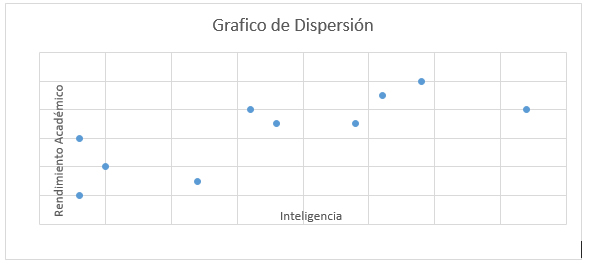
Una manera sencilla de identificar la correlación entre dos variables es a partir de una gráfica. 

Por ejemplo, se quiere saber si existe alguna relación entre lo siguiente:

  • Horas de estudio y calificación
  • Cantidad de alcohol ingerido y memoria
  • Peso de una persona y su inteligencia

Se grafica la nube de puntos y se puede ver si existe correlación fuerte o débil, positiva o negativa:

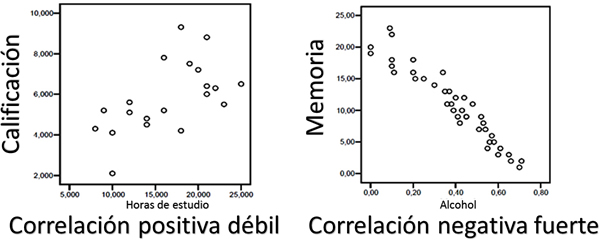
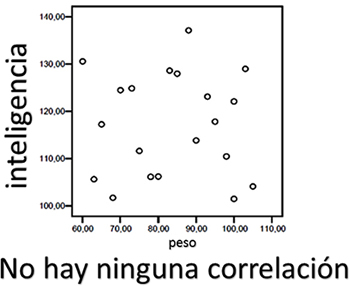
En la primer gráfica puedes observar que aun cuando las horas de estudio aportan un factor positivo hacia la calificación, no son determinantes, por lo cual la correlación entre calificación y horas de estudio es positiva débil. En el caso de la relación entre memoria e ingesta de alcohol se observa que sí hay una correlación negativa fuerte, lo que significa que a mayor cantidad de alcohol ingerida, menor memoria disponible. Al intentar relacionar inteligencia y peso, puedes observar que no existe ninguna correlación entre ellos porque los puntos están dispersos.

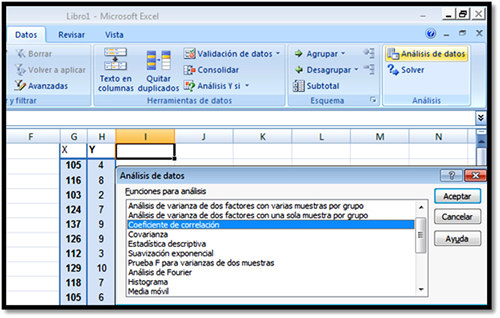
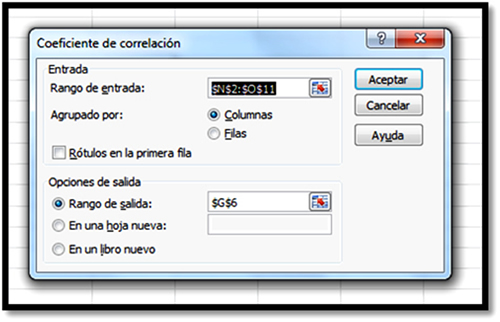
Para calificar el grado de correlación que existe en un conjunto de datos se utiliza el valor r, al que se denomina coeficiente de correlación de Pearson o correlación producto-momento. Se construye a partir de la siguiente relación matemática (Malhotra, 2008; Hair, 2007):

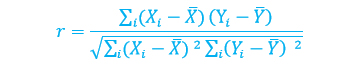
Si se divide numerador y denominador entre n – 1,  se obtiene:

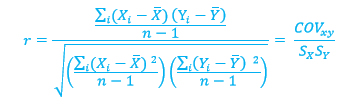
Las variables Y representan las medias muestrales y SX y SY  las desviaciones estándar. COVxy es la covarianza y mide el grado de relación entre X y Y. La covarianza puede ser positiva o negativa. La división entre SX SY  logra la estandarización, por lo que r  siempre estará entre -1 y +1. El coeficiente de correlación es un número, es decir, no lleva unidades y da indicación de qué tan bien relacionadas están las variables.

Para revisar un ejemplo, haz clic aquí.

Para construir el modelo lineal, de nuevo, puedes utilizar fórmulas (basadas en el método de mínimos cuadrados) o utilizar una herramienta computacional (por ejemplo Excel).
Las variables tienen una relación lineal, es decir, la relación entre ellas es de la forma Y = βo + β1X, donde βo será la ordenada al origen y β1 será la pendiente de la recta. Como no se conoce βo o β1, entonces a partir de la muestra se utilizan los datos para generar la ecuación lineal Ŷi = a + bxi  con Ŷi  valor estimado o predicho, a y b estimadores de βo y  β1 . 

Para encontrar la pendiente se utiliza la siguiente fórmula (Hair, 2007):

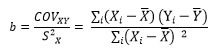
donde COV es la covarianza entre X eY y SX es la varianza de X.

Se aplican las fórmulas anteriores a los datos y se obtiene:

Pendiente 0.197463
Ordenada -16.7019027

 

 

Para resolver en Excel se procede como sigue:

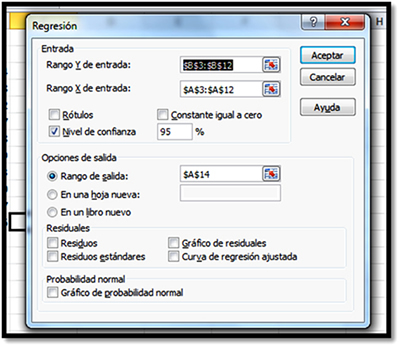
  1. Captura y selecciona los datos en Datos/Análisis de Datos/Regresión.
  2. En Rango Y de entrada selecciona, únicamente, datos de la variable dependiente y en Rango X de entrada selecciona, únicamente, datos de las variables independientes.
  3. Selecciona el nivel de confianza del 95% y si deseas el análisis de residuales o la gráfica de probabilidad normal, la seleccionas también.

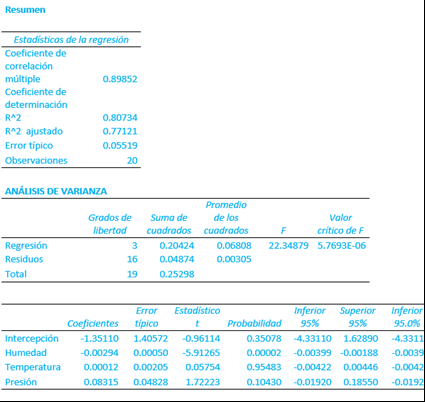
Los datos que arroja el análisis son los siguientes:

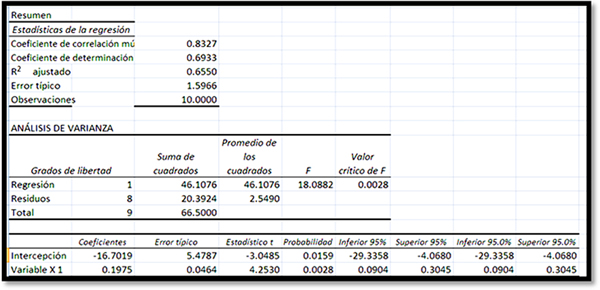
El coeficiente de correlación múltiple es r = 0.83267493. El coeficiente de determinación es r2 = 0.6933, que es un dato mayor a 0.5, por lo tanto es bueno. El coeficiente de determinación mide la proporción de la variación de una variable que está explicada por otra, es decir, da idea acerca del porcentaje de variabilidad que explica la propia variable. Esto significa que que cerca del 70% de la variabilidad es explicada por los datos del propio modelo.

Para armar el modelo lineal se utilizan los datos intercepción y variable X1, de donde se obtiene:

Y =  0.197463X1 – 16.7019027

Si se desea predecir qué calificación se espera de una persona con coeficiente intelectual de 120:

Y =  0.197463 (120) – 16.7019027=6.99

Ahora se quiere determinar qué coeficiente intelectual debe tener una persona que pretende obtener una calificación de 8.3:

8.3 = 0.197463(X1) – 16.7019027;     X1 = 126.61

Los otros parámetros, que se obtienen de los resultados, se analizarán más adelante en este mismo módulo.

Regresión múltiple

Cuando hay más de una variable independiente, muchas veces se cree que dejando ‘fija’ una de ellas y variando la otra es posible conocer el comportamiento del modelo en general, sin embargo, en general eso no conocer el modelo completamente. Por eso es conveniente aplicar la técnica de regresión múltiple.

Malhotra (2008) nos hace ver que la regresión múltiple implica una sola variable dependiente y dos o más variables independientes. Es la técnica estadística que simultáneamente desarrolla una relación matemática entre dos o más variables independientes y una variable dependiente de intervalo.

Los pasos del análisis de regresión múltiple son similares a los del análisis de regresión bivariada.

En este caso se busca un modelo lineal del tipo:

Ŷi = a + b1X1 + b2X2 + … + bkXk

En este caso, como se espera que X1 y X2 están correlacionadas, los coeficientes b1 b2 tendrán un comportamiento distinto. El coeficiente b1 representará el cambio esperado en Y para el cambio de una unidad en X1 ;  por su parte, b2 representará el cambio esperado en Y para el cambio de una unidad en X2.

En este caso, el cálculo de los coeficientes no es tan directo como en el análisis de correlación simple. Se puede pensar en eliminar el efecto de una de las variables independientes X2  sobre X1. Esto es posible haciendo un análisis de regresión de X1 sobre X2. Entonces el coeficiente de regresión parcial b1 es igual al coeficiente de regresión bR entre Y  y los residuales de X1 de donde se ha eliminado el efecto de X2.

Para revisar un ejemplo, haz clic aquí.

3.4 Métodos de diagnóstico

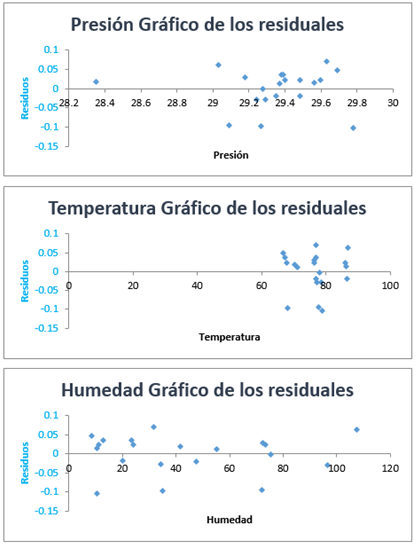
Pérez (2014) indica que el análisis de regresión lleva asociados, además, ciertos procedimientos de diagnóstico como el análisis de residuo, en donde se revisa gráficamente que las desviaciones estén dentro de cierto rango (ver gráficos residuales presentados anteriormente). Un residuo grande indica que la observación está lejos del modelo estimado y por lo tanto la predicción de esta observación es mala. 

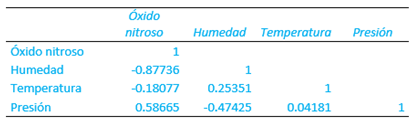
Otro método de diagnóstico es el gráfico de dispersión matricial, en donde se realiza el análisis de regresión por pares (similares a la matriz de correlación). Se muestra si hay algún par de variables que no tengan un comportamiento lineal.
Se puede elaborar un histograma de residuos a fin de observar si existe normalidad y simetría en la distribución de los residuos.

Cierre

El análisis de regresión se divide en simple y múltiple.

En el análisis de regresión simple se supone un comportamiento lineal entre la variable dependiente Y y la variable independiente X. En este caso el coeficiente de correlación da información acerca de la correlación que existe entre ellas. Si el índice es cercano a ‘±1’, puedes suponer que el modelo es lineal. Al encontrar la ecuación lineal que describe el comportamiento, podrás utilizarla para predecir el valor de Y para un determinado valor de X.

El análisis de regresión múltiple supone, también, un comportamiento lineal entre la variable dependiente Y  y las variables independientes Xi. Se utiliza la matriz de correlación para averiguar si las Xi están relacionadas entre sí. El coeficiente de correlación indicará si la Y es una combinación lineal de las Xi. La significancia de la ecuación de regresión general que se obtiene del análisis se evalúa con la prueba F. En el análisis de regresión múltiple también se supone que el modelo es lineal, si el índice de correlación es cercano a  ±1. En este análisis también el coeficiente de determinación r2 mide la proporción de la variación en una variable que está explicada por otra.

En el siguiente tema se completa el análisis que se ha iniciado aquí, porque a partir de las variaciones de los datos se buscará determinar, nuevamente, si un conjunto de datos tiene un comportamiento lineal o no y si se puede, entonces, generar una ecuación que permita predecir la Y a partir de datos Xi proporcionados.

Checkpoint

Antes de concluir el tema, asegúrate de poder contestar las preguntas que se enlistan a continuación.

Instrucciones: Haz clic en cada pregunta para conocer su respuesta.

El análisis de regresión se utiliza para varios propósitos, como la descripción de datos para encontrar relaciones lineales entre datos o predecir o estimar valores futuros. En la práctica todo esto es útil para los negocios que desean pronosticar ciertos eventos, hacer un análisis de gestión sobre la calidad de sus productos o simplemente describir datos de manera detallada, de tal forma que sean útiles para la toma de decisiones.

Los residuales son útiles para saber si el modelo se ajusta a los supuestos, o dicho de otra manera, para saber si está funcionando. Una forma de interpretarlo es a través del gráfico de los residuales: éstos deben presentar un patrón aleatorio; si no fuera así, la varianza no sería constante y el modelo no sería válido.

Referencias

Libro de texto:

  • Malhotra, N. (2008). Investigación de Mercados: Un enfoque aplicado. (5ª ed.) México: Pearson. 
    ISBN: 9789702611851

Libros de apoyo:

  • Malhotra, N. (2008). Investigación de Mercados: Un enfoque aplicado. (5ª ed.) México: Pearson. 
    ISBN: 9789702611851
  • Pérez, L.C. (2014). Técnicas de Análisis Multivariante de Datos. España: Pearson /Prentice.

Glosario

Coeficiente de determinación: es la fuerza de asociación y tiene un valor que varía entre 0 y 1. Corresponde al cuadrado del coeficiente de correlación r.  Indica la proporción de la variación total de Y que se explica por la variación de X.

Coeficiente de determinación múltiple: es la fuerza de la asociación que se mide usando el cuadrado del coeficiente de regresión múltiple.

Coeficiente de regresión: el parámetro estimado b generalmente se conoce como coeficiente de regresión no estandarizado.

Diagrama de dispersión: es una gráfica de los valores de dos variables para todos los casos u observaciones.

Error estándar de estimación: EEE  es la desviación estándar de los valores reales de Y a partir de los valores predictivos de Ŷ.

Error estándar: la desviación estándar de b, EEb.

Estadístico t: un estadístico t con n – 2 grados de libertad. Sirve para probar la hipótesis nula que plantea que no hay relación lineal entre X y X,  o Ho: β1 = 0, donde

Modelo de regresión bivariada: la ecuación básica de regresión es Yi = βo + β1 Xi + ei ; donde Y es la variable dependiente o de criterio, X es la variable independiente o predictiva, βo es la intersección de la línea, β1 es la pendiente de la línea y ei  es el error.

Prueba F: la prueba F se utiliza para probar la hipótesis nula que afirma que el coeficiente de determinación múltiple en la población R2  es igual a cero. El estadístico de prueba tiene una distribución F con k y (n – k – 1) grados de libertad.