2.1 Operaciones con matrices

Recuerda los siguientes conceptos de acuerdo a Hair (2007), primero que nada, qué es una matriz:
Una matriz es un objeto matemático de la forma:

Tiene como finalidad organizar datos interrelacionados en filas y columnas.
En amn el primer elemento m corresponde al número de fila, mientras que el segundo elemento n corresponde al número de columna.
La notación matricial es muy adecuada en la estadística multivariante, porque generalmente se analizan datos interrelacionados que conviene organizar y una matriz es un instrumento muy útil para esto. Observa el siguiente ejemplo de construcción de una matriz en un problema de programación lineal:
Se desea determinar una dieta que satisfaga los requerimientos nutricionales de un individuo. Se sabe que dicho individuo tiene requerimientos de 13 unidades de niacina, 15 unidades de tiamina y 45 unidades de vitamina C. Los alimentos que se proponen para la dieta son leche (con 3.2 unidades de niacina, 1.12 de tiamina y 32 de vitamina C), legumbres (con 4.9 unidades de niacina, 1.3 unidades de tiamina y 0 unidades de vitamina C), o naranjas (con 0.8 unidades de niacina, 0.19 de tiamina y 93 unidades de vitamina C).

¿Cómo construirías una matriz que permita identificar los alimentos y los nutrientes que cada uno aporta?

Como ves, con la matriz fácilmente se pueden identificar los requerimientos generales y las aportaciones de cada alimento, de tal forma que es muy útil para organizar datos. Cada columna contiene los datos correspondientes a leche, legumbres y naranja, y se denomina “vector columna”.
2.2 Distribución normal
Para Malhotra (2008), la distribución normal es una distribución de una variable aleatoria continua que presenta un solo pico, que es simétrica, cuya media µ está exactamente en el centro de la misma, cuya varianza σ representa el promedio de las desviaciones de las mediciones con respecto a su media µ y además que desciende hacia dos extremos que se acercan de forma asintótica al eje horizontal, pero no lo tocan:
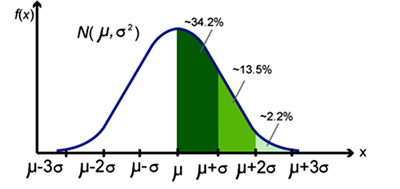
Imagen recuperada de http://www.etfos.hr/~akolundzic/slika-normalna-razdioba-ses.gif Sólo para fines educativos
La curva o distribución normal es muy utilizada en conjuntos de datos porque muchos fenómenos se distribuyen de esa forma; por ejemplo, distribución de estaturas de una población, consumo de productos en un grupo determinado de personas, cociente intelectual, puntuaciones de un examen, efectos de una misma dosis de un fármaco, entre otros. A su representación se le llama también “Campana de Gauss”.
Ahora bien, cuando un conjunto de datos obedece a una distribución normal, la media µ y la varianza σ serán los parámetros que la determinarán. Para ello se realiza un procedimiento que se llama normalización, que significa un corrimiento de la media µ hacia el valor cero, de tal forma que pueda hacerse uso de tablas de distribución Z para determinar la probabilidad.
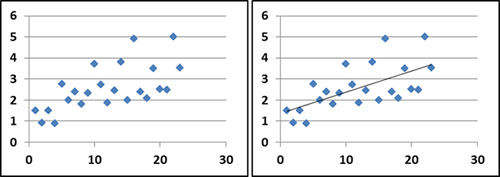
Para normalizar una serie de datos de los cuales se conocen la media µ y la varianza σ, se utiliza la siguiente fórmula: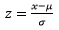 , en donde x es la variable tipificada (elemento a probar), µ es la media y σ es la varianza.
, en donde x es la variable tipificada (elemento a probar), µ es la media y σ es la varianza.
Cuando se realiza la normalización de datos, fácilmente se puede encontrar el área bajo la curva de la gráfica de la distribución, que representa la probabilidad y que está calculada en tablas. Si no se hiciera una normalización, se tendría que obtener la integral de la función normal (el área bajo la curva), que es una función muy difícil de integrar.
2.3 Coeficiente de correlación
Al análisis que se realiza si la nube de puntos se puede ajustar a una línea recta, se le denomina regresión lineal. Dos variables estadísticas están correlacionadas si al cambiar una cambia la otra. El parámetro que se utiliza para determinar qué tan relacionadas están entre ellas se denomina índice o coeficiente de correlación (r). El coeficiente de correlación será siempre un valor que esté entre -1 y 1, es decir: -1 < r < 1. Si |r| es cercano a 1, entonces hay una correlación fuerte y si |r| es cercano a 0, la correlación será débil (Malhotra, 2008).
Cuando los datos tienden a una línea recta se puede hacer un análisis para encontrar la ecuación de dicha recta (denominada recta de regresión). La ecuación puede servir para hacer estimaciones de datos futuros (Malhotra, 2008; Pérez 2014).
Ejemplo:
Se desea saber si existe alguna relación entre la temperatura corporal y la frecuencia cardíaca de un grupo de 12 personas:
| Persona |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Temperatura (°F) |
96.3 |
97.4 |
98.9 |
99 |
99 |
96.8 |
98.4 |
98.4 |
98.8 |
98.8 |
99.2 |
99.3 |
| Frecuencia cardíaca (pulsos/min) |
70 |
68 |
80 |
75 |
79 |
75 |
74 |
84 |
73 |
84 |
66 |
68 |
Con un gráfico de dispersión de puntos se puede saber si existe una correlación entre ambas variables:
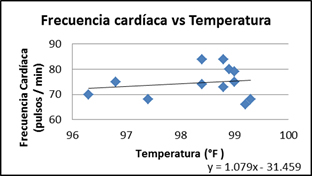
Se puede observar que no hay una relación ni una tendencia clara entre los puntos.
El coeficiente de correlación r es de 0.1740, lo cual determina que la correlación es prácticamente inexistente.
Ecuación de la recta ajustada: 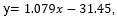 que se obtiene encontrando la recta de la línea de tendencia de los puntos.
que se obtiene encontrando la recta de la línea de tendencia de los puntos.







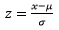 , en donde x es la variable tipificada (elemento a probar), µ es la media y σ es la varianza.
, en donde x es la variable tipificada (elemento a probar), µ es la media y σ es la varianza.


