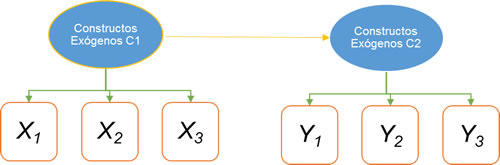
El modelo de ecuaciones estructurales (SEM) es un procedimiento para calcular una serie de relaciones de dependencia entre un conjunto de conceptos o construcciones representada por múltiples variables medidas e incorporado en un modelo integrado (Malhotra, 2010).
Los aspectos distintivos del SEM son (Malhotra, 2010):
Como podrá constatarse los SEM están conformados por un modelo de medida y un modelo estructural. El primero obedece las reglas del análisis de factores; mientras que el segundo obedece al funcionamiento del análisis de senderos (path analysis) (Malhotra, 2010; Hair, 2007).
15.1 Variables latentes
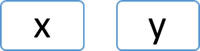
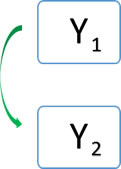
Las variables manifiestas u observables son aquellas que se miden directamente. Así pues, llevan este nombre si y sólo si su valor se obtiene mediante un experimento muestral real. Se representan es a través de cuadrados o rectángulos. En general se les asignan las letras X y Y.
Las variables latentes o no observables son aquéllas que no pueden ser medidas directamente. Entonces, cualquier variable que no pueda ser directamente observada debe ser considerada como no observable. Se puede decir que hablamos sobre variables abstractas, que representan conceptos unidimensionales (Malhotra, 2010; Hair, 2007).
Entonces, ya que las variables latentes corresponden a conceptos, son variables hipotéticas que varían en su grado de abstracción. La inteligencia, la clase social, el poder y las expectativas, son ejemplos de variables latentes abstractas creadas en la teoría.
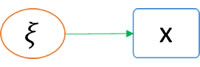
Las variables latentes necesitan ser medidas a través de variables observadas. Para representarlas se utilizan círculos o elipses. En general se determinan con las letras griegas ξ y η, según su función en el modelo exógena o endógena respectivamente.
Las relaciones entre variables se muestran con flechas. Si son unidireccionales representan la hipótesis de un efecto directo de una variable sobre otra. El origen de la flecha indica la causa; la punta, el efecto (Hair, 2007).
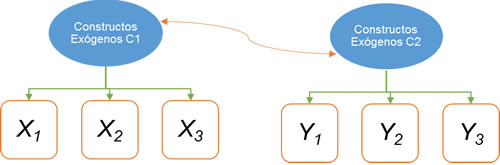
Cuando hay relaciones recíprocas entre las variables la relación se representa con dos flechas o una fecha con puntas en ambos lados (Malhotra, 2010; Hair, 2007).
La correlación entre dos variables se representa con una flecha curva bidireccional (Malhotra, 2010; Hair, 2007).
Los errores se representan como si fueran una variable, indicando la variable con la que están relacionados. Teóricamente, los errores representan todas las causas de una variable que son omitidas. Los errores se consideran variables latentes.
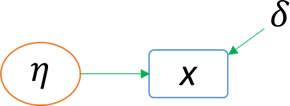
Variable exógena, independiente, regresora o predictora es aquélla cuyas causas son desconocidas. Se determinan fuera del modelo para que influyan en el comportamiento de las variables endógenas. Se identifican porque no reciben impactos, sólo salen flechas (Hair, 2007).
Las variables endógenas, dependientes o de criterio se caracterizan por ser explicadas por el funcionamiento del modelo; son explicadas por las variables exógenas propuestas e identifican por recibir impactos de otras variables (Malhotra, 2010; Hair, 2007).
En los modelos estructurales es posible que una variable tenga doble función, como endógena y exógena. A esta doble función se le conoce como efecto indirecto o mediador.
Instrucciones: Haz clic en cada punto para conocer la relación.
- Relación de dependencia
- Relación de correlación
15.2 Validación del modelo conceptual
Los pasos para realizar un modelo SEM son los siguientes:
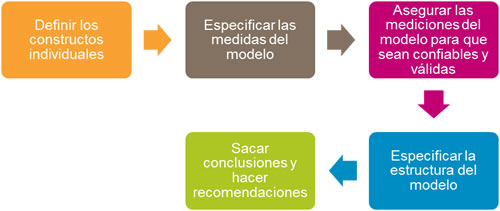
Asegurar la validez del modelo estructural involucre (1) examinar el ajuste, (2) comparar el modelo estructural propuesto con modelos competidores y (d) probar la relación estructural y las hipótesis.
Existen múltiples indicadores de ajuste que pueden ser utilizados para probar la bondad de ajuste del modelo (Malhotra, 2010; Hair, 2007). Éstos deben incluir:
- El valor de x2 y sus grados de libertad asociados:
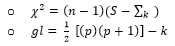
- Dos índices absolutos de ajuste:
- Un índice de bondad de ajuste (GFI, AGFI)
- Un índice de maldad de ajuste (RMSR, SRMR, RMSEA)
- Un índice incremental de ajuste (CFI, TLI, NFI,NNFI, RNI)
- Un índice parsimónico de ajuste para modelos de diferentes complejidades (PGFI, PNFI)
La identificación de modelo se refiere a si hay suficiente información en la matriz de covarianza para permitirnos estimar un conjunto de ecuaciones estructurales. Podemos estimar un parámetro para cada variación única o covariación entre las variables observadas. Si hay p variables observadas, hasta un máximo de (p(p + 1)) / 2 parámetros pueden estimarse. Tenga en cuenta que este número es la suma de todas la covarianza única (p(p – 1)/2) y todas las varianzas, p. Por lo tanto, (p(p + 1)) / 2 = p(p – 1)/2 + p.
Si calcula que si el número real de los parámetros, k, es menos de (p(p + 1)) / 2, el modelo está sobreidentificado. En ese caso, tenemos grados de libertad positivos. Por el contrario, si es mayor de k, (p(p + 1)) / 2, el modelo está subidentificado y no puede encontrarse una solución única. Como pauta general, tener por lo menos tres variables observadas para cada constructo latente ayuda en la identificación del modelo, es decir, se traduce en un modelo sobreidentificado. Esta práctica, por lo tanto, se recomienda.
15.3 “Path Analysis”
El Análisis de Senderos (Path Analysis) es el modelo más utilizado para verificar y apoyar conjuntos de supuestos causales entre variables que se estudian. Su objetivo es explicar las variables dependientes y la relación existente entre ellas. Sólo se consideran variables observables (Malhotra, 2010; Hair, 2007).
Las variables dependientes tienen asociado un error aleatorio llamado disturbio. Los disturbios son semejantes a los residuales en una regresión, pero su connotación está más basada en un modelo causal que en un modelo de predicción. Teóricamente, representan las causas de variables endógenas que son omitidas en el modelo estructural.
Si el modelo construido se ajusta a los datos, el modelo se mantiene con el fin de ser sometido a nuevas pruebas, o bien, para modificarlo o reemplazarlo. En cualquier caso, el análisis de senderos no es un procedimiento para demostrar la existencia de causalidad en forma definitiva.
El análisis de senderos inicia con un diagrama basado en una teoría, mismo que señala las relaciones de influencias sobre las variables. Se busca validar o no la hipótesis expuesta en la estructura causal, así como evaluar el peso de cada relación, a través de los llamados coeficientes de sendero (Hair, 2007).
Los modelos de senderos se pueden clasificar en recursivos y no recursivos. En los recursivos los disturbios no están correlacionados y todos los efectos causales son unidireccionales. Los no recursivos tienen causalidad recíproca y los disturbios pueden estar correlacionados.
Un modelo de Path Analysis o Análisis de Senderos se representa matemáticamente con la ecuación siguiente (Hair, 2007):
Donde
X = vector de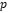 
× 1 de variables observadas independientes
Y = vector de 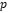× 1 de variables observadas dependientes
B = matriz de 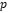× 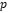de coeficientes correspondientes a Y
Γ = matriz de 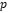× 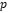de coeficientes correspondientes a X
ζ = vector de 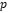× 1 de disturbios
15.4 Pruebas de mediación y moderación
Pruebas de mediación
Cuando existe una variable interpuesta entre la variable independiente y la dependiente se conoce como causalidad mediadora. Esta variable mediadora es a su vez dependiente de la primera e independiente de la segunda. En la mediación, la variable intermedia ayuda a explicar cómo o por qué una variable independiente influye en un resultado (Malhotra, 2010; Hair, 2007).
Algunas consideraciones a tener para minimizar la mediación:
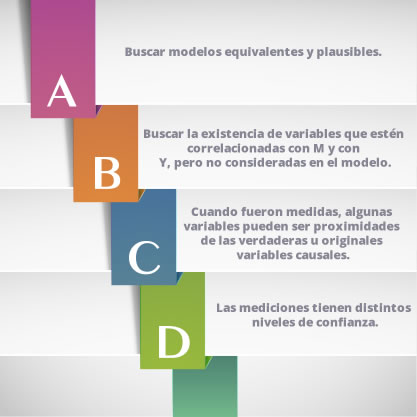
Pruebas de moderación
Cuando se introduce una variable independiente adicional como producto de dos variables independientes del modelo se produce el efecto de moderación.
Cuando la moderación influye la medición de manera continua, esta influencia generalmente provoca que en el modelo se cree una nueva variable que es producto de la variable siendo moderada (X) y la variable que está moderando (W). Esta interacción (XW) es entonces introducida en la ecuación de regresión después de que su principal efecto (Y) de la moderación (W) y variable moderada (X) fue estimado (Malhotra, 2010; Hair, 2007).
Si el efecto de XW es significativo, entonces el efecto de X sobre Y es dependiente a los niveles de W. Existe un simple procedimiento que permite dar un peso a los estimados de la regresión de la ecuación completa y graficar un número de regresiones implicadas con la intención de proveer una visualización del efecto moderador.
