10.1 Conceptos y objetivo básico del análisis discriminante

Malhotra (2008) describe el análisis discriminante como una técnica multivariante que se puede utilizar para generar reglas con las que se puede hacer la clasificación de una población agrupada. El análisis discriminante es similar al análisis de regresión, a excepción de que, en este caso, la variable dependiente es categórica (no métrica) en vez de continua. Por esta razón, el análisis discriminante nos permitirá predecir la pertenencia a una clase, de una observación particular, con base en un conjunto de variables predictoras.

Los objetivos de esta técnica son los siguientes (Malhotra, 2008):

Instrucciones: Haz clic para ver a detalle cada dimensión

A continuación se presentan los supuestos que fundamentan esta técnica:

• Cada grupo debe ser una muestra de una población normal multivariada.
• Las matrices de covarianza poblacional deben ser iguales, es decir, la dispersión de los datos con respecto a su media y la dispersión de los datos teniendo en cuenta las dos variables como si fueran una sola, son iguales.

10.2 Clasificación del análisis discriminante: simple y múltiple

El análisis discriminante de dos grupos, en el que la variable dependiente sólo tiene dos categorías, está muy relacionado con el análisis de regresión múltiple. Si la variable dependiente es métrica con valores 0 o 1 (binaria), entonces se puede hacer el tratamiento de análisis de regresión, que es mucho más simple para resolver. A este modelo se le denomina modelo logit. (Luque, 2012).

10.3 Cálculo de la función discriminante

El modelo de análisis discriminante supone combinaciones lineales del siguiente tipo (Malhotra, 2008):

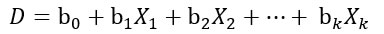
Donde:

D = calificación discriminante

b = coeficiente o peso discriminante

X = variable independiente o predictiva

Los coeficientes se calculan de forma tal que el grupo difiera, tanto como sea posible, en los valores de la función discriminante, lo cual ocurre cuando es máxima la razón de la suma de cuadrados entre grupos y la suma de cuadrados intragrupos de las puntuaciones discriminantes.

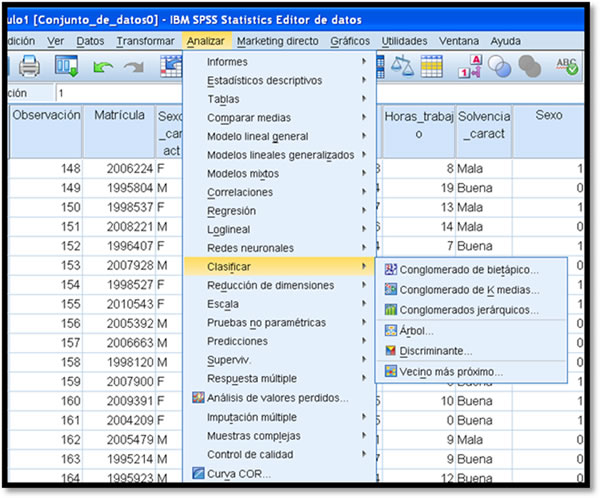
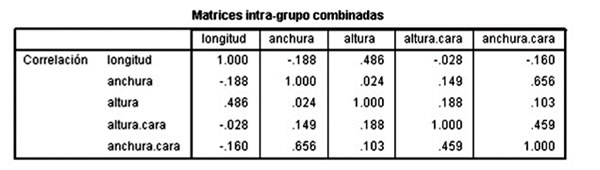
Esas diferencias se obtienen a partir de la matriz de relaciones que se puede obtener en el paquete estadístico que estemos utilizando, en el cual se encuentra como matriz de correlación (ver cuadros en PSPP en el ejemplo) (Pérez, 2004). La matriz de correlación se presenta en PSPP de la siguiente forma:

Matrices intragrupo combinadas

Las suposiciones del análisis discriminante se trata de que cada uno de los grupos es una muestra de una población normal multivariada y todas las poblaciones tienen la misma matriz de covarianza (Malhotra, 2008). El papel de estas suposiciones y los estadísticos pueden entenderse mejor si se revisa el algoritmo para realizar el análisis discriminante:

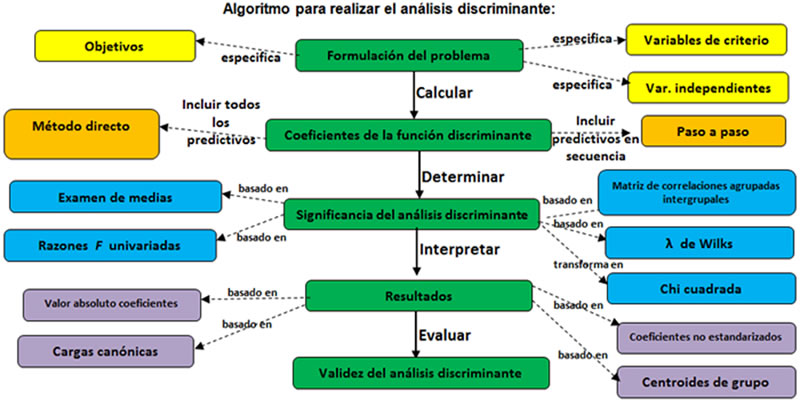
Formulación del problema. En la formulación del problema se identifican los objetivos del análisis discriminante, las variables de criterio y las variables independientes. Las variables de criterio tendrán que ser al menos dos variables mutuamente excluyentes entre sí. Cuando la variable dependiente se basa en una escala de intervalo o de razón, se tendrá que convertir en categoría en primer lugar. Por ejemplo, en una encuesta hacia la simpatía a cierto partido político, en la escala de 7 puntos podrá categorizarse como desfavorable (1, 2, 3), neutra (4) o favorable (5, 6, 7), de tal forma que sea posible graficar la distribución de la variable dependiente y formar grupos de igual tamaño.

El siguiente paso es dividir la muestra en dos partes. Una parte de la muestra, llamada muestra de análisis o de estimación, se utiliza para calcular la función discriminante. Otra parte de la muestra, llamada muestra de validación o de exclusión, se reserva para la validación de la función discriminante. Es muy conveniente repetir la validación del análisis discriminante a fin de asegurarnos de los resultados adecuados. En este caso conviene dividir la muestra en forma diferente y volver a validar. Cuando utilizamos un paquete computacional, muchas veces realiza la validación de forma automática (Luque, 2012; Malhotra, 2008; Hair, 2007; Pérez 2004).

Cálculo de coeficientes de la función discriminante 

Para determinar los coeficientes de la función discriminante existen dos métodos generales:

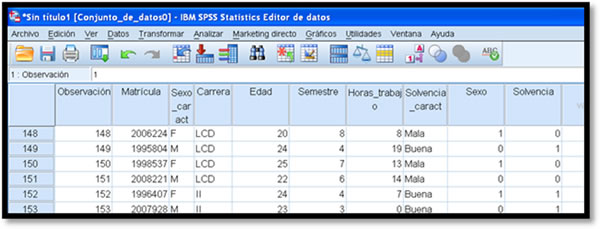
En el paquete computacional (PSPP, Excel u otro) se anotan dos tablas: una con los datos a discriminar y otra con los datos que darán validez al análisis. Estos datos se seleccionan de forma aleatoria.

Para revisar un ejemplo, haz clic aquí.

Pruebas de significancia estadística

Significancia de análisis discriminante. Es indispensable realizar alguna de estas pruebas a fin de determinar si las funciones discriminantes calculadas son estadísticamente significativas (Malhotra, 2008; Hair, 2007; Pérez, 2004). Existen varias pruebas que podemos realizar, a continuación se presentan algunas de ellas:

1. El examen de medias, en éste se espera que se rechace la hipótesis nula de que todas las medias sean iguales.
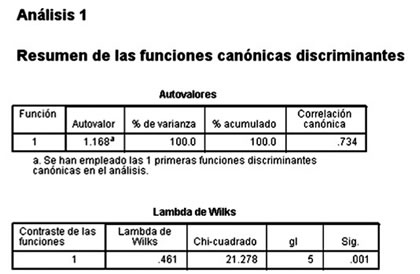
2. La λ de Wilks, es el producto de la λ univariada de cada función (y es la prueba que realiza el paquete PSPP). El cálculo del nivel de significancia se basa en la transformación del estadístico en una chi cuadrada. Si la λ es pequeña, entonces discrimina mucho; la variabilidad total se debe a las diferencias entre grupos, no a las diferencias dentro de grupos.
3. El cálculo del estadístico F, se basa en una aproximación a la distribución de la razón de probabilidad, en donde se compara, para cada variable, las desviaciones de las medias de cada uno de los grupos con respecto a la media total (y es la prueba que hace SAS). Si F es grande para cada variable, entonces las medias de cada grupo están muy separadas y la variable discrimina bien.
4. La matriz de correlaciones agrupadas intergrupales indica correlaciones bajas entre los predictivos, de tal forma que cada variable será independiente.

Interpretación de resultados. La interpretación de los pesos o coeficientes discriminantes es similar al método de regresión múltiple. El valor del coeficiente para un predictivo depende de los otros incluidos en la función discriminante. Existen distintos elementos para poder interpretar los resultados en un análisis multivariante, algunos de ellos son los siguientes:

• Las cargas canónicas: representan la varianza que el predictivo comparte con la función. Cuanto mayor sea la magnitud de una correlación estructural, mayor será la importancia del predictivo correspondiente.
• Los coeficientes estandarizados: representan las intercorrelaciones entre los predictivos, y se usan como multiplicadores cuando las variables se han estandarizado con una media de 0 y una varianza de 1.
• Los coeficientes no estandarizados: sirven simplemente para clasificación.
• Los centroides de grupo: indican el valor de la función discriminante evaluada en las medias del grupo. Los signos de los coeficientes asociados son positivos, mientras que los no asociados son negativos.

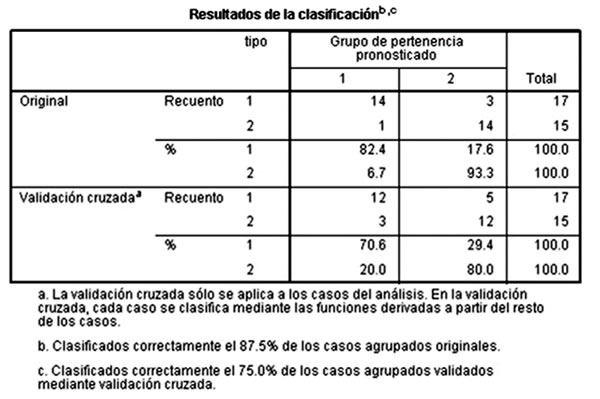
Validación del modelo

El dato que se use en la validez de análisis discriminante dependerá del paquete computacional utilizado. En el caso de PSPP se ofrece la opción de validación cruzada con exclusión, lo cual significa que cada vez se excluye a un encuestado y el modelo se utiliza para predecir los datos sobre este encuestado. Eso da solidez a los cálculos de los estadísticos. Al final del análisis aparece la siguiente leyenda: “Clasificados correctamente el…% de los datos agrupados originales…, “Clasificados correctamente el…% de los datos agrupados validados”, con lo cual podemos garantizar la validez de nuestro análisis (Malhotra, 2008).

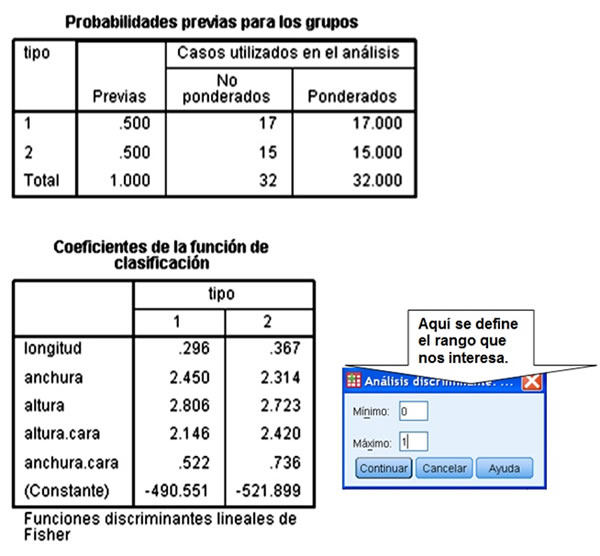
Finalmente, armamos la función discriminante a partir de los coeficientes no estandarizados de nuestro análisis, tal y como aparecen en la tabla de coeficientes de clasificación en cuestión que arroja PSPP, de manera que obtendremos los datos para formar una expresión del tipo:

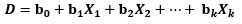
Si alguno de los coeficientes es significativamente menor al resto, se puede descartar influir en los grupos.

En conclusión, el análisis discriminante es una técnica muy útil para poder separar o eliminar aquellas variables que no sean indispensables para caracterizar una muestra. También el análisis discriminante es útil para determinar si hay diferencia entre varios grupos de datos, a partir de una variable categórica dependiente de otras variables métricas independientes.

El análisis discriminante es una técnica muy útil para clasificar y separar grupos con determinada característica, para probar si existen diferencias significativas entre la media de los perfiles de la variable predictora de los dos grupos o para determinar cuáles variables explican más las diferencias intergrupos en la media de perfiles. 

Existen dos métodos para realizar el análisis discriminante: 1) paso a paso, se van discriminando las variables una por una, y 2) método directo, se incluyen todos los predictivos simultáneamente.

De acuerdo al número de categorías, tenemos el análisis discriminante de dos grupos (técnica en que la variable de criterio tiene dos categorías) y el análisis discriminante múltiple (técnica en que la variable de criterio tiene tres o más categorías).

Así, el análisis discriminante es útil para examinar datos cuando la variable de criterio es categórica y las variables independientes son métricas. Éste consta de cinco pasos básicos, que son los siguientes:

1. Formulación del problema.
2. Cálculo de los predictivos, que generalmente se realiza en un software estadístico.
3. Determinación de la significancia estadística para probar la hipótesis nula de que todas las medias de las muestras son iguales. Se debe rechazar la hipótesis nula para poder interpretar los resultados.
4. Interpretación de pesos o coeficientes discriminantes.
5. Validación.

Para llevar a cabo el análisis discriminante, existen dos métodos generales: directo y paso a paso. Cuando se tiene idea de la variable a discriminar se puede usar el último método.

Antes de concluir el tema, asegúrate de poder contestar las preguntas que se enlistan a continuación.

Instrucciones: Haz clic en cada pregunta para conocer su respuesta.

Calificación de discriminación: los coeficientes no estandarizados se multiplican por los valores de las variables. Los productos se suman y se agregan al término constante para obtener la calificación de discriminación.

Centroide: el centroide es la media de las calificaciones discriminantes de un grupo particular. Existen tantos centroides como grupos, porque hay uno para cada grupo. Los centroides de grupo son las medias de ese grupo en todas las funciones.

Coeficientes de la función discriminante: los coeficientes (no estandarizados) de la función discriminante son los multiplicadores de las variables, cuando éstas se encuentran en las unidades de medición originales.

Coeficientes estandarizados de la función discriminante: son los que suelen usarse como multiplicadores cuando las variables se han estandarizado con una media de 0 y una varianza de 1.

Estructura de correlaciones: también conocida como cargas discriminantes, la estructura de correlaciones representa las correlaciones simples entre los predictivos y la función discriminante.

Matriz de clasificación (matriz de confusión o de predicción): contiene el número de casos cuya clasificación fue correcta e incorrecta. Los casos bien clasificados aparecen en la diagonal porque los grupos reales y los pronosticados son los mismos. Los elementos fuera de la diagonal representan casos cuya clasificación fue incorrecta. La suma de los elementos de la diagonal, dividida entre el número total de casos, representa la proporción de aciertos.

Matriz de correlaciones agrupadas intragrupales: para calcular la matriz de correlaciones agrupadas intragrupales se promedian las matrices de covarianza separadas de todos los grupos.

Valor propio: para cada función discriminante, el valor propio es la razón de la suma de cuadrados entre grupos e intragrupos. Los valores grandes suponen funciones superiores.

Valores F y su significancia: se calculan en un ANOVA de una vía, donde la variable de agrupamiento es la variable independiente categórica. A la vez, en el ANOVA, cada predictivo funge como variable dependiente métrica.

 de Wilks: conocida también como estadístico U. La  de Wilks de cada predictivo es la razón entre la suma de los cuadrados intragrupo y la suma total de los cuadrados. Su valor fluctúa entre 0 y 1. Los valores grandes de  indican que parece haber diferencia entre las medias del grupo. 

Libro de texto:

• Malhotra, N. (2008). Investigación de Mercados: Un enfoque aplicado. (5ª ed.) México: Pearson. 
  ISBN: 9789702611851

Libros de apoyo:

• Hair, J. F. (2007). Análisis Multivariante. (5ª ed.). México: Pearson/ Prentice Hall.
  ISBN: 9788483220351. 
  
• Pérez, L.C. (2014). Técnicas de Análisis Multivariante de Datos. España: Pearson /Prentice.