1.1 Definición de estadística multivariante
De acuerdo a Hair (2007), la estadística multivariante es la parte de la estadística y del análisis de datos que estudia, analiza, representa e interpreta los datos que resultan de observar un número de variables estadísticas sobre una muestra de individuos.
El único supuesto es que las variables observables son homogéneas y correlacionadas sin que haya predominio de alguna sobre las demás.
Como la información estadística tiene características multidimensionales, para su manejo se requieren herramientas como la geometría, el cálculo matricial y las distribuciones multivariantes.
Los datos que se adquieren en la estadística multivariante a menudo sirven para alimentar matrices de distancias o de similitudes que miden el grado de acercamiento o alejamiento entre datos de la muestra.
La estadística multivariante tiene su origen en 1809, cuando Gauss desarrolló el uso de la regresión lineal y más tarde, en 1900, con el modelo oculto de Markov. A pesar de que las técnicas usadas hoy en día tienen su origen en 1930, no fue sino hasta mediados del siglo XX, con el desarrollo de computadoras, paquetes estadísticos y econométricos, que estos métodos lograron popularidad.
1.2 Escalas de medición y tipos de datos
El análisis de los datos significa clasificación, identificación y medición de un conjunto de variables y sus variaciones, tanto aquéllas que se dan entre ellas mismas como las que suceden entre una variable dependiente y una o más variables independientes (Malhotra, 2008).
Malhotra explica que “Medida” es la palabra clave para que el investigador pueda identificar una variación, sobre todo si ésta no es cuantificable. La medida representará el valor por el cual se selecciona el método de análisis multivariado apropiado.
Existen dos tipos básicos de datos:
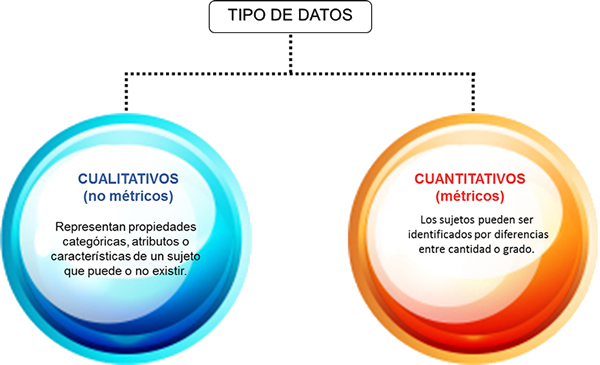
En el caso de los datos no métricos las propiedades del sujeto son mutuamente excluyentes (por ejemplo, si es hombre, no puede ser mujer). Aquí no hay cantidad sino condición. Existen escalas nominales que sirven para etiquetar sujetos según cierta característica que presentan o no (por ejemplo, para identificar sexo, religión, partido político, alguna forma de comportamiento o acción); también existen escalas ordinales con las que se puede medir cierto parámetro (grado de satisfacción hacia un producto, por ejemplo) de acuerdo a una escala.
Los datos métricos son mejores para casos en que las diferencias son cuantificables y pueden clasificarse como de intervalo y de razón. Las escalas de razón representan el más alto grado de precisión, porque relacionan un punto de la escala con otro de forma exacta.
Ejemplos de datos de intervalo: recorre del kilómetro 50 al 125; pesa 55 kg; está en los 50.
Ejemplos de datos de razón: 30 K (grados Kelvin, donde hay un cero absoluto); $50 de salario (donde hay una referencia a $0 de salario) o 20 m (donde hay una referencia a 0 m).
Los datos se pueden ejemplificar en el siguiente diagrama:
Hair (2007) indica que debemos suponer que todas las variables que se usan en las técnicas multivariantes tendrán algún grado de error y además que los valores de correlación que se obtengan podrán estar afectadas por ese error. El error de medida será también muy importante en la estadística multivariante porque representará el grado en el cual los valores reportados no son valores reales.
Ahora bien, un error de medida puede tener su origen en imprecisión a la hora de medir; una respuesta errónea que proporcione un encuestado o por cualquier otra circunstancia en donde datos erróneos se toman como adecuados.
La obligación del investigador es reducir el error de medida, por lo que deberá cuidar los aspectos de validez y de fiabilidad de la medida. El investigador también puede utilizar escalas sumadas en donde distintas variables se unen a una medida compuesta (por ejemplo, el total de puntos en una prueba psicológica). La idea es usar diferentes variables como indicadores que representen distintas facetas del concepto, para tener una perspectiva más completa.
Por ejemplo, para ordenar las áreas básicas de salud en cierta región, de acuerdo a sus características socioeconómicas, se construye un indicador de necesidad relativa que incluye distintos parámetros, como cantidad de clínicas, distancias de la comunidad a los centros de salud, número de personas que trabajan en esos centros, etcétera.
La mayoría de las técnicas multivariantes se basan en la inferencia estadística. Se parte de una hipótesis nula y se busca determinar el grado de confianza, como el nivel de error permitido (recuerda las definiciones de error tipo I y error tipo II provistas en el glosario del tema anterior).
Tipos de técnicas multivariantes y su objetivo
Acorde a Malhotra (2008), los métodos de estadística multivariante se diferenciarán de acuerdo al área de aplicación, al número de variables y a la manera en que estén distribuidos los datos.
Existen distintos tipos de técnicas multivariantes:
- En los métodos de dependencia el objetivo es determinar si el conjunto de variables independientes afecta al conjunto de variables dependientes y de qué manera. Como ejemplo de una técnica de análisis que conlleve una dependencia técnica está el análisis de regresión múltiple, el análisis conjunto, el análisis discriminante o el análisis de varianza (MANOVA).
- En los métodos de interdependencia el objetivo es identificar qué variables están relacionadas, cómo se relacionan y por qué se relacionan. Como ejemplo de una técnica de análisis en el cual todas las variables del conjunto se toman simultáneamente está el análisis factorial.
- En los métodos estructurales el objetivo es analizar no sólo cómo afectan las variables independientes a las variables dependientes, sino también cómo se relacionan las variables de los dos grupos entre sí.
1.3 Objetivos y clasificación de las técnicas multivariables:
Objetivos
De acuerdo a Hair (2007), los objetivos de la estadística multivariable son los siguientes:
- Proporcionar métodos cuya finalidad es el estudio del conjunto de datos multivariantes que el análisis estadístico unidimensional y bidimensional no pueden conseguir.
- Ayudar al analista o investigador a tomar decisiones óptimas en el contexto en el que se encuentre, teniendo en cuenta la información disponible por el conjunto de datos analizado.
Clasificación
Malhotra (2008) proporciona la siguiente clasificación de las técnicas multivariables:
Instrucciones: Haz clic en cada dimensión para ver el detalle
Se utiliza para analizar variables interrelacionadas entre un gran número de variables y para explicarlas en términos de valores comunes llamados “factores”. El objetivo de este análisis es encontrar la manera de condensar la información contenida en un número original de variables en un número más pequeño, sin perder información.
Ejemplo: para determinar el o los factores que propician el nacimiento de bebés de bajo peso entre madre fumadora, situaciones familiares y enfermedades preexistentes de la madre.
Se utiliza para explorar simultáneamente relaciones entre varias variables independientes categóricas (llamadas tratamientos) y dos o más variables dependientes métricas. Representa una extensión del análisis de varianza univariado (ANOVA).
Ejemplo: en una muestra sirve para determinar si existe alguna diferencia en la solución de un test de acuerdo a la escolaridad de los examinados.
Aunque las emociones son inherentes al ser humano, anteriormente eran medidas únicamente con fines médicos. A partir de hace algunos años se encontró la utilidad estadística de cuantificar las emociones, percepciones y sentimientos para fines mercadológicos.
Ejemplo: para verificar si un perfume en particular genera ciertas emociones al ser percibido.
Se utiliza cuando el problema a investigar presenta una variable métrica dependiente y dos o más variables métricas independientes. El objetivo es predecir cambios en la variable dependiente como respuesta a cambios en las variables independientes. El método de solución se basa en mínimos cuadrados.
Ejemplo: para relacionar la cantidad de trigo producida según la cantidad de precipitación y la cantidad de fertilizante aplicada a cierta cosecha.
Es una técnica cuyo objetivo es determinar qué combinación de un número limitado de características es la favorita de una muestra de encuestados. Se utiliza frecuentemente para comprobar la aceptación de diseños de nuevos productos y el atractivo de la publicidad. Se supone que un producto tiene determinadas características o atributos y distintos niveles para cada uno de éstos; los encuestados evalúan el cuestionario a fin de decidir qué producto es su favorito. Esas respuestas llevan al diseño del mejor producto.
Ejemplo: a partir de las preferencias en las características de un grupo de zapatos deportivos se determinan atributos deseables para diseñar un nuevo par de zapatos, que se ofrecerán posteriormente al mercado.
Esta herramienta es muy útil cuando se cuenta con bases de datos muy extensas con información (textual o numérica) de un grupo de personas. Esta herramienta busca “adentrarse” en las profundidades de esta información tratando de encontrar analogías entre los casos que ayuden a predecir comportamientos o bien, a describir diversos aspectos relacionados.
Ejemplo: un banco que tiene información sobre todos sus clientes puede llegar a predecir si un cliente nuevo que solicita un crédito es candidato viable para otorgarlo o no.
Se utiliza si la única variable dependiente es dicotómica (es decir, cuando sólo puede tomar dos valores: mujer/hombre) o multicotómica (chico/mediano/grande), que es una variable no métrica. Por su parte las variables independientes son métricas. El análisis discriminante es aplicable a situaciones en donde la muestra total puede dividirse en grupos clasificados por los valores de la variable dependiente.
Ejemplo: puede mostrar diferencias y similitudes entre cráneos encontrados en distintas regiones del Tíbet, a partir de mediciones como longitud de cara, ancho y altura de cara.
Es una técnica analítica en donde se seleccionan subgrupos significativos de individuos u objetos y se clasifican en entidades muestra. Se van reduciendo con base en similitudes entre las mismas entidades. A diferencia del análisis discriminante, los grupos no están predefinidos sino que precisamente se busca identificarlos.
Ejemplo: para identificar de forma geográfica los sitios más susceptibles de sufrir dengue o malaria.
En muchas ocasiones una decisión final no se toma basándose en un solo criterio; más bien, existen múltiples causas que llevan a una consecuencia. Poder relacionar todos esos aspectos que llevan a algo implica la creación de un modelo y en ese sentido, las ecuaciones estructurales ayudarán para saber si éste es válido o no.
Ejemplo: para identificar la forma en que la satisfacción del cliente se va generando desde la experiencia en la tienda hasta después del uso de un producto en particular; qué aspectos están involucrados, qué va primero y qué después y cómo se interrelacionan entre sí todos estos aspectos.
1.4 Algoritmo para la construcción de un modelo multivariante
En general, Hair (2007) indica que para construir un modelo de estadística multivariante debes seguir los siguientes pasos:
- Definir el problema a investigar así como los objetivos y la técnica multivariante a utilizar. En esta parte se determina si se busca agrupar, seleccionar y determinar coincidencias o elaborar un tipo de función, ya que eso establece el tipo de análisis, así como sus objetivos.
- Desarrollar el plan de análisis que depende del tipo de técnica a aplicar a los datos.
- Evaluar los supuestos, ya que todas las técnicas multivariantes se aplican de acuerdo a supuestos específicos.
- Hacer una estimación del modelo multivariantey evaluar ajustes, la cual provee los valores obtenidos para las variables o el rango de valores permitidos para éstas. En caso de que los resultados no concuerden, se puede replantear el problema.
- Interpretar las variantes a través de parámetros particulares de cada método multivariante.
- Validar el modelo multivariante. Generalmente se hace mediante estadísticos, como la chi cuadrada, que garantizan poblaciones de comportamiento normal o algún otro particular del método.
Para cada uno de los modelos multivariantes se verá el algoritmo en particular a fin de poder resolverlo con éxito.







